オペアンプの回路例

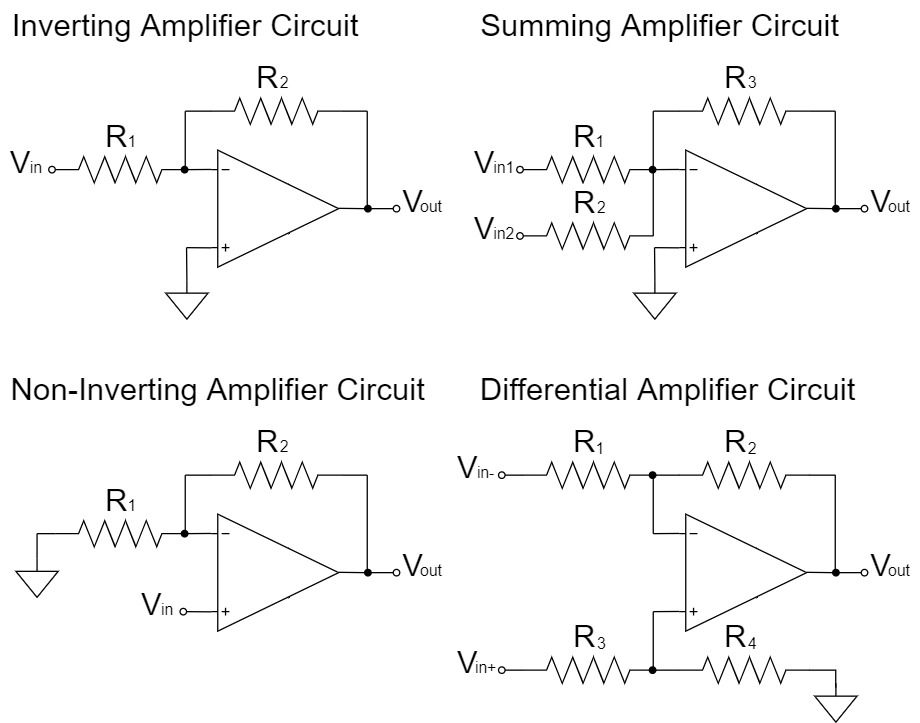
当記事では、比較的よく使われるオペアンプ(OPアンプ/OP-Amp)の回路を紹介していきます。

さらに、それぞれの回路ごとの詳しい解説は、リンク先の個別の記事にまとめているので、ぜひご覧ください。

増幅回路

増幅回路とは、小さい信号を大きい信号に変えるための回路です。

オペアンプの増幅回路は、2本の抵抗の値により簡単に増幅率を設定でき、トランジスタと比較して増幅度(ゲイン)も非常に大きく設計することができます。

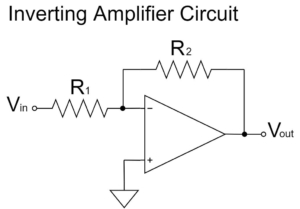
反転増幅回路

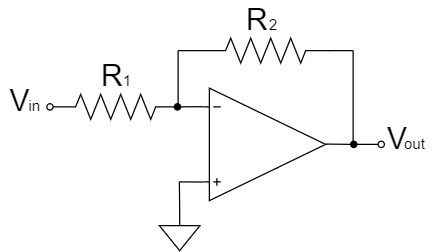
$$V_{out}=-\frac{R_2}{R_1}V_{in}$$
反転増幅回路は、上式の通り、$\frac{R_2}{R_1}$の増幅率で、$V_{in}$の信号が増幅され、$V_{out}$に出力されます。また、「$-$」の極性が表す通り、$V_{out}$の信号は反転されます。

例えば、$R_1=1kΩ, R_2=10kΩ, V_{in}=1V$であれば、$V_{out}=-10V$になります。
$$V_{out}=-\frac{10k}{1k} \times 1=-10[V]$$
オペアンプの反転増幅回路のさらに詳しい解説は以下の記事をご覧下さい。

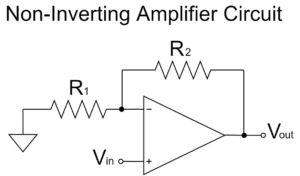
非反転増幅回路

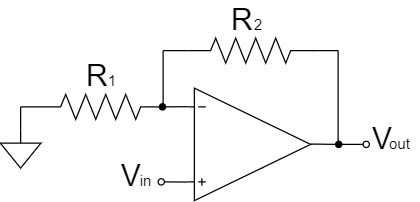
$$V_{out}=\left(1+\frac{R_2}{R_1}\right)V_{in}$$
非反転増幅回路は、上式の通り、$1+\frac{R_2}{R_1}$の増幅率で、$V_{in}$の信号が増幅され、$V_{out}$に出力されます。

例えば、$R_1=1kΩ, R_2=10kΩ, V_{in}=1V$であれば、$V_{out}=11V$になります。
$$V_{out}=\left(1+\frac{10k}{1k}\right) \times 1=11[V]$$
オペアンプの非反転増幅回路のさらに詳しい解説は以下の記事をご覧下さい。

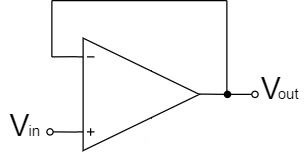
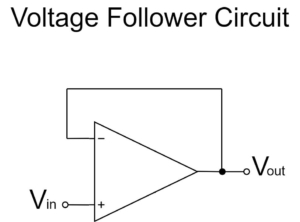
電圧フォロワ(ボルテージフォロワ)

$$V_{out}=V_{in}$$
電圧フォロワ(ボルテージフォロワ)は、上式の通り、$V_{in}$の信号と全く同じ電圧が$V_{out}$に出力されます。

非反転増幅回路では、増幅率1倍を回路を作れないので、代わりに電圧フォロワを使います。

例えば、$V_{in}=1V$であれば、$V_{out}=1V$になります。
$$V_{out}=1[V]$$
オペアンプの電圧フォロワ(ボルテージフォロワ)のさらに詳しい解説は以下の記事をご覧下さい。

演算回路

演算回路とは、複数の信号を足したり、引いたりするなど演算(計算)するための回路です。

オペアンプの演算回路は、反転増幅回路などの基本的な回路を、一部、変更・追加することで作ることができるので、トランジスタと比較して簡単に設計することができます。

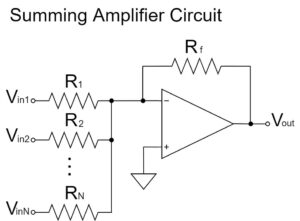
加算回路

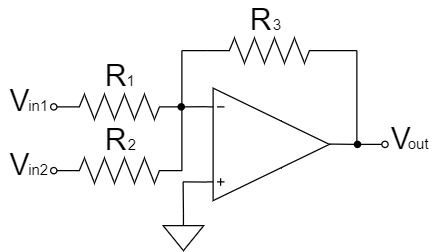
$$V_{out}=-R_3\left(\frac{V_{in1}}{R_1}+\frac{V_{in2}}{R_2}\right)$$
加算回路は、反転増幅回路の入力側の抵抗に、さらに並列で抵抗を追加した回路です。

上式の通り、複数の入力信号を加算して出力します。抵抗比による重み付けが必要ない場合、$R_1=R_2=R_3$であれば、入力信号の電圧を加算した値が、反転してそのまま出力電圧となるのでわかりやすいです。

例えば、$R_1=R_2=R_3=10kΩ, V_{in1}=3V, V_{in2}=7V$であれば、$V_{out}=-10V$になります。
$$V_{out}=-10k\left(\frac{3}{10k}+\frac{7}{10k}\right)=-10[V]$$
オペアンプの加算回路のさらに詳しい解説は以下の記事をご覧下さい。

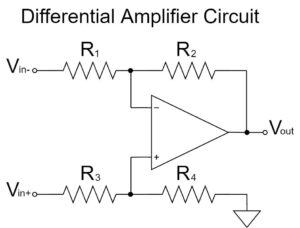
減算回路(差動増幅回路)

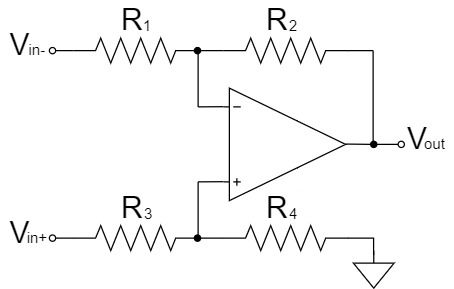
$$V_{out}=\frac{R_2}{R_1}\left(V_{in+}-V_{in-}\right)$$
減算回路は、2つの入力信号の差分(減算値)を増幅することから、差動増幅回路とも呼ばれます。

上式の通り、$R_1=R_3, R_2=R_4$であれば、$\frac{R_2}{R_1}$の増幅率で、$V_{in+}-V_{in-}$の信号が増幅され、$V_{out}$に出力されます。

例えば、$R_1=R_2=R_3=R_4=10kΩ, V_{in+}=12V, V_{in-}=2V$であれば、$V_{out}=10V$になります。
$$V_{out}=\frac{10k}{10k}\left(12-2\right)=10[V]$$
オペアンプの減算回路(差動増幅回路)のさらに詳しい解説は以下の記事をご覧下さい。

比較回路(コンパレータ)

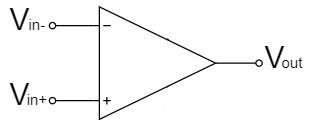
$$V_{out}=+V_{CC} \quad (V_{in+}>V_{in-})$$
$$V_{out}=-V_{CC} \quad (V_{in+} \lt V_{in-})$$
比較回路(コンパレータ)は、負帰還をかけずに、開ループで動作させます。

非反転入力$V_{in+}$と反転入力$V_{in-}$の大小関係に従って出力が決まるので、上式の通り、$V_{in+}>V_{in-}$の時は+側の電源電圧$+V_{CC}$で飽和し、$V_{in+} \lt V_{in-}$の時は-側の電源電圧$-V_{CC}$で飽和します。

ただ、実際の使い方としては、今まで説明したような別個の2つの電圧を比較するより、一方の入力に基準電圧を与え、もう一方の入力に加えられる入力電圧を基準電圧と比較する使い方が多いです。

以下のように、大きくわけて、入力電圧を反転入力または非反転入力にする回路があります。出力電圧が反転するしないの違いだけで特性的な違いはありません。

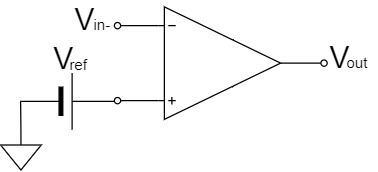
$$V_{out}=-V_{CC} \quad (V_{in-}>V_{ref})$$
$$V_{out}=+V_{CC} \quad (V_{in-} \lt V_{ref})$$
まず、入力電圧を反転入力にした場合、上式の通り、$V_{in-}>V_{ref}$の時は-側の電源電圧$-V_{CC}$で飽和し、$V_{in-} \lt V_{ref}$の時は+側の電源電圧$+V_{CC}$で飽和します。

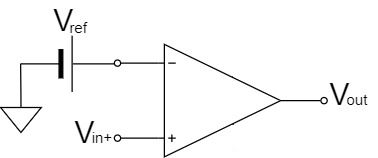
$$V_{out}=+V_{CC} \quad (V_{in+}>V_{ref})$$
$$V_{out}=-V_{CC} \quad (V_{in+} \lt V_{ref})$$
次に、入力電圧を非反転入力にした場合、上式の通り、$V_{in+}>V_{ref}$の時は+側の電源電圧$+V_{CC}$で飽和し、$V_{in+} \lt V_{ref}$の時は-側の電源電圧$-V_{CC}$で飽和します。

オペアンプの比較回路(コンパレータ)のさらに詳しい解説は以下の記事をご覧下さい。

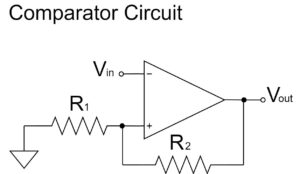
ヒステリシス付き比較回路(ヒステリシス付きコンパレータ)

開ループで動作する比較回路(コンパレータ)に正帰還をかけることで、基準電圧にヒステリシス特性を持たせることができます。

以下のように、大きくわけて、入力電圧を反転入力または非反転入力にする回路があります。$V_{refH}$と$V_{refL}$の計算方法がそれぞれの回路で異なるので注意して下さい。

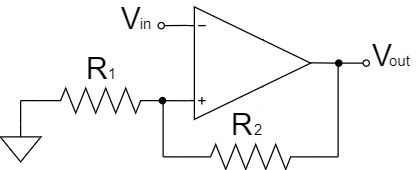
$$V_{out}=-V_{CC} \quad (V_{in-}>V_{refH}) \quad V_{refH}=\frac{R_1}{R_1+R_2}V_{CC}$$
$$V_{out}=+V_{CC} \quad (V_{in-} \lt V_{refL}) \quad V_{refL}=-\frac{R_1}{R_1+R_2}V_{CC}$$
まず、入力電圧を反転入力にした場合、上式の通り、$V_{in-}>V_{refH}$の時は-側の電源電圧$-V_{CC}$で飽和し、$V_{in-} \lt V_{refL}$の時は+側の電源電圧$+V_{CC}$で飽和します。

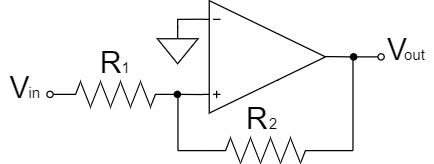
$$V_{out}=+V_{CC} \quad (V_{in+}>V_{refH}) \quad V_{refH}=\frac{R_1}{R_2}V_{CC}$$
$$V_{out}=-V_{CC} \quad (V_{in+} \lt V_{refL}) \quad V_{refL}=-\frac{R_1}{R_2}V_{CC}$$
次に、入力電圧を非反転入力にした場合、上式の通り、$V_{in+}>V_{refH}$の時は+側の電源電圧$+V_{CC}$で飽和し、$V_{in+} \lt V_{refL}$の時は-側の電源電圧$-V_{CC}$で飽和します。

入力信号にノイズが含まれている場合、ばたつきを防ぐため、比較回路にヒステリシス特性は必須となります。

しきい値付近でノイズが発生すると、ヒステリシス特性がないと出力がばたついてしまいます。

一方、ヒステリシス特性がついていると、$V_{refH}$と$V_{refL}$の間であれば出力がばたつかなくなります。

オペアンプのヒステリシス付き比較回路(ヒステリシス付きコンパレータ)のさらに詳しい解説は以下の記事をご覧下さい。

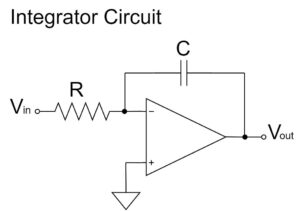
完全積分回路

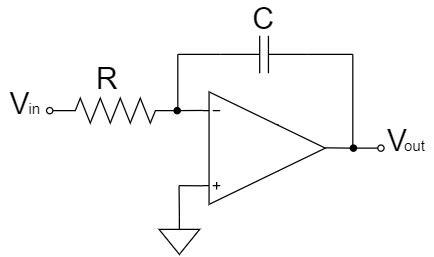
$$V_{out}=-\frac{1}{CR} \int V_{in}dt$$
完全積分回路は、反転増幅回路の帰還抵抗が、コンデンサに置き換わった回路です。

上式の通り、$\frac{1}{CR}$の増幅率で、入力電圧$V_{in}$の積分値が増幅され、出力電圧$V_{out}$に出力されます。また、「$-$」の極性が表す通り、出力電圧$V_{out}$の信号は反転されます。

そのため、入力電圧$V_{in}$が直流の場合、積分回路の出力電圧$V_{out}$は時間の経過に比例して増加していきますが、オペアンプの取り扱いできる電圧上限の電源電圧で飽和します。

また、入力電圧$V_{in}$が交流の場合、周波数が高くなるにつれて利得が$-20[dB/dec](-6[dB/oct])$の傾きで減少していき、カットオフ周波数$f_C$の時点で$0[dB]$となります。

このように、直流電圧を入力すると、出力電圧が電源電圧の上限に飽和してしまい、交流電圧を入力すると、どの周波数帯でも利得が一定にならないことから、あまり実用で使われることはありません。

オペアンプの完全積分回路のさらに詳しい解説は以下の記事をご覧下さい。

不完全積分回路

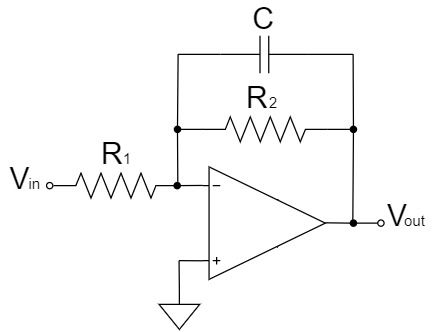
$$V_{out}=-\frac{R_2}{R_1}V_{in} \quad (f_{in} \ll f_C)$$

$$V_{out}=-\frac{1}{CR_1} \int V_{in}dt \quad (f_{in} \gg f_C)$$

$$f_C=\frac{1}{2πCR_2}$$

不完全積分回路は、反転増幅回路の帰還抵抗にコンデンサが並列接続された回路です。

上式の通り、入力周波数$f_{in}$がカットオフ周波数$f_C$より十分に小さい場合$(f_{in} \ll f_C)$は反転増幅回路、入力周波数$f_{in}$がカットオフ周波数$f_C$より十分に大きい場合$(f_{in} \gg f_C)$は完全積分回路として動作します。

主な使用方法としては、波形変換とローパスフィルタの用途があります。

波形変換は、積分領域$(f_{in} \gg f_C)$に入力して使います。

また、ローパスフィルタは、通過させたい信号を非積分領域$(f_{in} \ll f_C)$、除去したい信号を積分領域$(f_{in} \gg f_C)$に入力して使います。

オペアンプの不完全積分回路のさらに詳しい解説は以下の記事をご覧下さい。

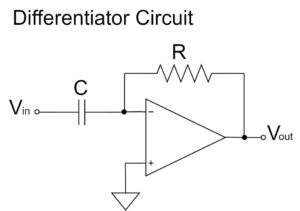
完全微分回路

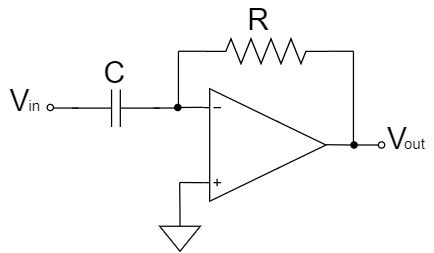
$$V_{out}=-CR\frac{dV_{in}}{dt}$$
完全微分回路は、反転増幅回路の入力側の抵抗が、コンデンサに置き換わった回路です。

上式の通り、$CR$の増幅率で、入力電圧$V_{in}$の微分値が増幅され、出力電圧$V_{out}$に出力されます。また、「$-$」の極性が表す通り、出力電圧$V_{out}$の信号は反転されます。

そのため、入力電圧$V_{in}$が変化せず一定(直流)だと、出力電圧$V_{out}$は$0V$のままになり、$V_{in}$が変化(傾斜)の大きいと、その傾斜に比例した電圧が$V_{out}$に出力されます。

例えば、三角波を微分回路に入力すると、方形波が出力します。三角波の傾斜が大きい場合、積分回路と同様、電源電圧で飽和することになります。

また、入力電圧$V_{in}$が交流の場合、周波数が高くなるにつれて利得が$20[dB/dec](6[dB/oct])$の傾きで増加していき、カットオフ周波数$f_C$の時点で$0[dB]$となります。

このように、完全積分回路と違って出力電圧が電源電圧の上限に飽和してしまうことはありませんが、周波数の高いわずかなノイズでも増幅してしまうことから、あまり実用で使われることはありません。

オペアンプの完全微分回路のさらに詳しい解説は以下の記事をご覧下さい。

不完全微分回路

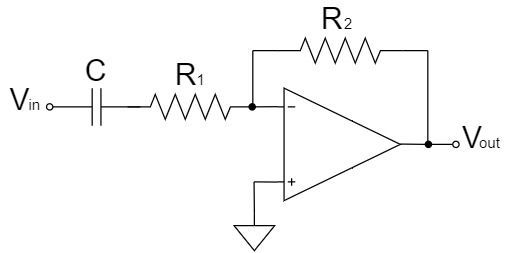
$$V_{out}=-\frac{R_2}{R_1}V_{in} \quad (f_{in} \gg f_C)$$

$$V_{out}=-CR\frac{dV_{in}}{dt} \quad (f_{in} \ll f_C)$$

$$f_C=\frac{1}{2πCR_2}$$

不完全微分回路は、反転増幅回路の入力抵抗にコンデンサが直列接続された回路です。

上式の通り、入力周波数$f_{in}$がカットオフ周波数$f_C$より十分に大きい場合$(f_{in} \gg f_C)$は反転増幅回路、入力周波数$f_{in}$がカットオフ周波数$f_C$より十分に小さい場合$(f_{in} \ll f_C)$は完全微分回路として動作します。

主な使用方法としては、方形波のエッジ検出とハイパスフィルタの用途があります。

方形波のエッジ検出は、微分領域$(f_{in} \ll f_C)$に入力して使います。

また、ハイパスフィルタは、通過させたい信号を非積分領域$(f_{in} \gg f_C)$、除去したい信号を積分領域$(f_{in} \gg f_C)$に入力して使います。

オペアンプの不完全微分回路のさらに詳しい解説は以下の記事をご覧下さい。