オペアンプの微分回路
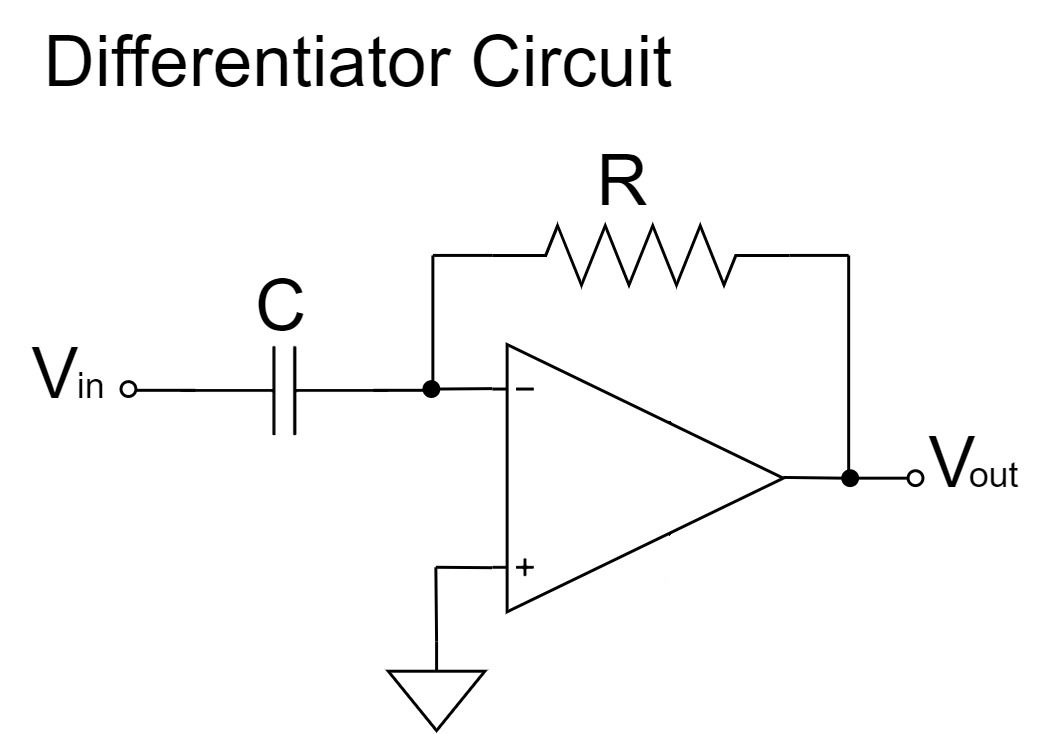
当記事では、「オペアンプ(OPアンプ/OP-Amp)の微分回路」について詳しく解説していきます。
微分回路は、オペアンプの反転増幅回路を応用したもので、入力抵抗をコンデンサに置き換えると「完全微分回路」、入力抵抗にコンデンサを直列接続すると「不完全微分回路」となります。
オペアンプの微分回路の特徴
「完全微分回路」と「不完全微分回路」にわけて、オペアンプの微分回路の特徴について解説していきます。
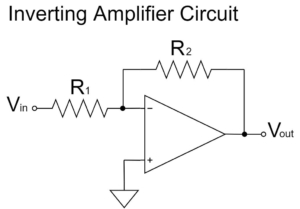
なお、今回、説明するオペアンプの微分回路は、オペアンプの反転増幅回路を応用したものなので、先に反転増幅回路について勉強しておいた方が理解がしやすいです。
オペアンプの反転増幅回路の詳しい解説は以下の記事をご覧下さい。
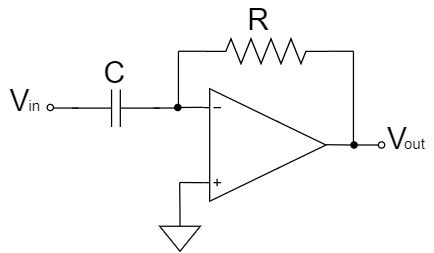
完全微分回路
$$V_{out}=-CR\frac{dV_{in}}{dt}$$
完全微分回路は、反転増幅回路の入力側の抵抗が、コンデンサに置き換わった回路です。
上式の通り、$CR$の増幅率で、入力電圧$V_{in}$の微分値が増幅され、出力電圧$V_{out}$に出力されます。また、「$-$」の極性が表す通り、出力電圧$V_{out}$の信号は反転されます。
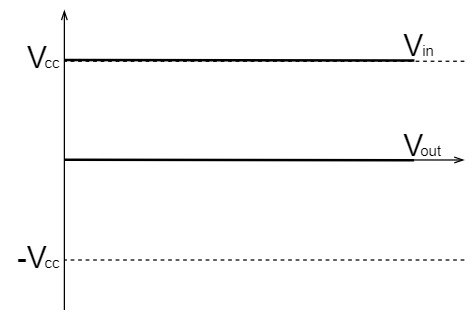
そのため、入力電圧$V_{in}$が変化せず一定(直流)だと、出力電圧$V_{out}$は$0V$のままになり、$V_{in}$が変化(傾斜)の大きいと、その傾斜に比例した電圧が$V_{out}$に出力されます。
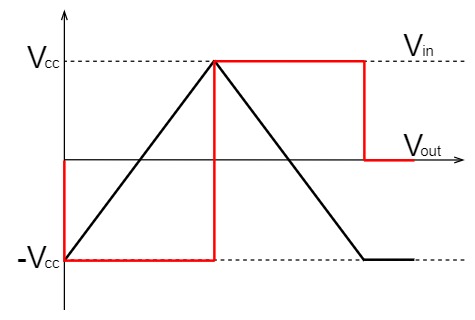
例えば、三角波を微分回路に入力すると、方形波が出力します。三角波の傾斜が大きい場合、積分回路と同様、電源電圧で飽和することになります。
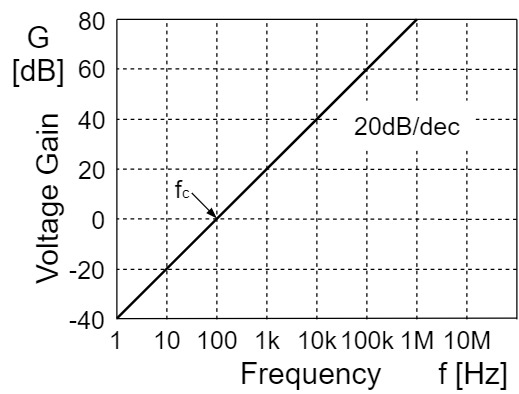
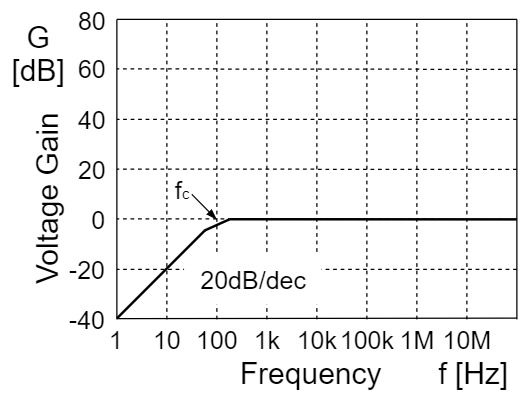
また、入力電圧$V_{in}$が交流の場合、周波数が高くなるにつれて利得が$20[dB/dec](6[dB/oct])$の傾きで増加していき、カットオフ周波数$f_C$の時点で$0[dB]$となります。
このように、完全積分回路と違って出力電圧が電源電圧の上限に飽和してしまうことはありませんが、周波数の高いわずかなノイズでも増幅してしまうことから、あまり実用で使われることはありません。
不完全微分回路
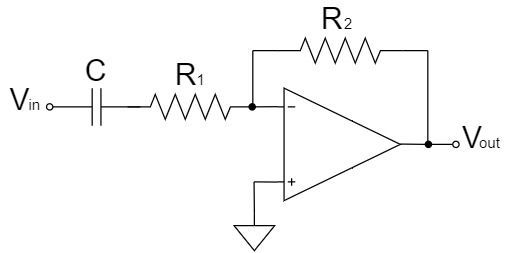
$$V_{out}=-\frac{R_2}{R_1}V_{in} \quad (f_{in} \gg f_C)$$
$$V_{out}=-CR\frac{dV_{in}}{dt} \quad (f_{in} \ll f_C)$$
$$f_C=\frac{1}{2πCR_2}$$
不完全微分回路は、反転増幅回路の入力抵抗にコンデンサが直列接続された回路です。
上式の通り、入力周波数$f_{in}$がカットオフ周波数$f_C$より十分に大きい場合$(f_{in} \gg f_C)$は反転増幅回路、入力周波数$f_{in}$がカットオフ周波数$f_C$より十分に小さい場合$(f_{in} \ll f_C)$は完全微分回路として動作します。
主な使用方法としては、方形波のエッジ検出とハイパスフィルタの用途があります。
方形波のエッジ検出は、微分領域$(f_{in} \ll f_C)$に入力して使います。
また、ハイパスフィルタは、通過させたい信号を非積分領域$(f_{in} \gg f_C)$、除去したい信号を積分領域$(f_{in} \gg f_C)$に入力して使います。
オペアンプの完全微分回路の計算
オペアンプの完全微分回路の関係式を求めるために、回路各部の電圧の関係式から算出する精密計算と理想オペアンプをヌラーモデルに置き換えた簡易計算をします。
オペアンプの不完全微分回路については、「オペアンプの微分回路の特徴」-「不完全微分回路」で解説した通り、$f_{in} \gg f_C$は反転増幅回路の関係式、$f_{in} \ll f_C$は完全微分回路の関係式と覚えておきましょう。
精密計算1
オペアンプの回路図記号
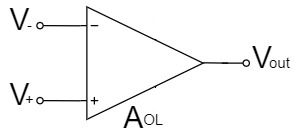
オペアンプは、$V_+$と$V_-$の2つの入力電圧の電位差をオープンループゲイン$A_{OL}$(開放利得$A_{OL}$)で増幅します。
$$V_{out}=A_{OL}(V_+-V_-)$$
完全微分回路
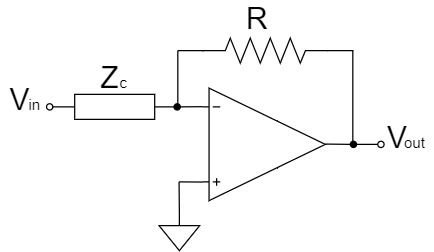
完全微分回路は反転増幅回路の入力抵抗がコンデンサに置き換わったと考えることができるので、わかりやすくするため$C$をインピーダンスの$Z_C$とみなして計算していきます。
この完全微分回路の場合、$+$端子がGNDに接続されているので、$V_+$は0[V]になります。
$$V_+=0$$
以上により、完全微分回路の$V_{out}$は以下のようになります。
$$V_{out}=A_{OL}(0-V_-)=-A_{OL}V_-\cdots(1)$$
また、オペアンプの$-$端子は入力インピーダンスが高く、電流が流れ込まないことから、以下のような回路で表すことができます。
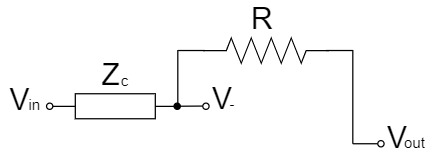
重ね合わせの理(重ね合わせの原理、重ねの理、重畳の理)により、上記の回路を2つに分割して考えると、分圧回路として簡単に$V_-$を求めることができます。
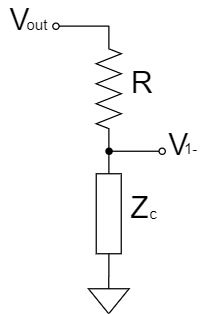
$$V_{1-}=\frac{Z_C}{Z_C+R}V_{out}$$
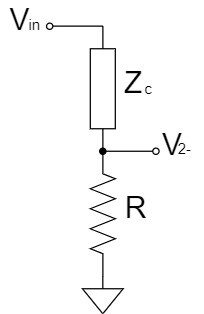
$$V_{2-}=\frac{R}{Z_C+R}V_{in}$$
よって、$V_-$は以下のようになります。
$$V_{-}=V_{1-}+V_{2-}$$
$$V_-=\frac{Z_C}{Z_C+R}V_{out}+\frac{R}{Z_C+R}V_{in}\cdots(2)$$
(1)式に(2)式を代入することで、$V_{out}$を計算していきます。
$$V_{out}=-A_{OL}\left(\frac{Z_C}{Z_C+R}V_{out}+\frac{R}{Z_C+R}V_{in}\right)$$
$$V_{out}=-\frac{Z_C}{Z_C+R}A_{OL}V_{out}-\frac{R}{Z_C+R}A_{OL}V_{in}$$
$$V_{out}+\frac{Z_C}{Z_C+R}A_{OL}V_{out}=-\frac{R}{Z_C+R}A_{OL}V_{in}$$
$$\frac{Z_C+R}{Z_C+R}V_{out}+\frac{A_{OL}Z_C}{Z_C+R}V_{out}=-\frac{R}{Z_C+R}A_{OL}V_{in}$$
$$\frac{Z_C+R+A_{OL}Z_C}{Z_C+R}V_{out}=-\frac{R}{Z_C+R}A_{OL}V_{in}$$
$$V_{out}=-\frac{R}{Z_C+R+A_{OL}Z_C}A_{OL}V_{in}$$
$$V_{out}=-\frac{A_{OL}R}{Z_C+R+A_{OL}Z_C}V_{in}$$
$$V_{out}=-\frac{R}{Z_C}\frac{A_{OL}}{1+\frac{R}{Z_C}+A_{OL}}V_{in}$$
$$V_{out}=-\frac{R}{Z_C}\frac{1}{\frac{1}{A_{OL}}+\frac{1}{A_{OL}}\frac{R}{Z_C}+1}V_{in}$$
$$V_{out}=-\frac{R}{Z_C}\frac{1}{\frac{1}{A_{OL}}(1+\frac{R}{Z_C})+1}V_{in}$$
ここで、$A_{OL}$は極めて大きい値(∞)であることを考えると、$\frac{1}{A_{OL}}⇒0$になります。よって、$V_{out}$は以下のようになります。
$$V_{out}=-\frac{R}{Z_C}V_{in}$$
ここまでは反転増幅回路の計算と同じでしたが、さらに$Z_C$の部分を計算します。コンデンサのインピーダンス$\frac{1}{jωC}$を$Z_C$に代入すると以下のようになります。
$$V_{out}=-\frac{R}{\frac{1}{jωC}}V_{in}=-jωCRV_{in}\cdots(3)$$
$\frac{1}{jω}$は位相が90°遅れ、周波数が高くなるほど値が低くなることを表す複素数の虚部になります。複素数は三角関数または指数関数で表すことができ、オイラーの公式により以下のような関係があります。
$$e^{jθ}=cosθ+jsinθ$$
$θ[rad], ω[rad/s], t[s]$の関係は$θ=ωt$なので、オイラーの公式は以下のように表すこともできます。$$e^{jωt}=cosωt+jsinωt$$
また、底がネイピア数$e$である指数関数は微分・積分しても変化しない性質を持っています。
$$\frac{d}{dx}e^{x}=e^{x}$$
$$\int e^{x}dx=e^{x}$$
そのため、$e^{jωt}$を微分すると、以下のようになります。
$$\frac{d}{dt}e^{jωt}=jω\frac{d}{d(jωt)}e^{jωt}=jωe^{jωt}$$
つまり、微分と$jω$の関係は以下のようになることがわかります。
$$\frac{d}{dt}=jω$$
よって、$\frac{d}{dt}=jω$を(3)式に代入することで最終的な$V_{out}$は以下のようになります。
$$V_{out}=-jωCRV_{in}=-CR\frac{dV_{in}}{dt}$$
精密計算2
完全微分回路

完全微分回路は反転増幅回路の入力抵抗がコンデンサに置き換わったと考えることができるので、わかりやすくするため$C$をインピーダンスの$Z_C$とみなして計算していきます。
この完全微分回路の場合、$+$端子がGNDに接続されているので、$V_+$は0[V]になります。
$$V_+=0$$
さらに、$+$と$-$の端子は、仮想短絡(イマジナリショート/バーチャルショート)を通じて接続されていると考えることができます。
$$V_-=V_+=0\cdots(1)$$
また、オペアンプの$-$端子は入力インピーダンスが高く、電流が流れ込まないことから、以下のような回路で表すことができます。

重ね合わせの理(重ね合わせの原理、重ねの理、重畳の理)により、上記の回路を2つに分割して考えると、分圧回路として簡単に$V_-$を求めることができます。

$$V_{1-}=\frac{Z_C}{Z_C+R}V_{out}$$

$$V_{2-}=\frac{R}{Z_C+R}V_{in}$$
よって、$V_-$は以下のようになります。
$$V_{-}=V_{1-}+V_{2-}$$
$$V_-=\frac{Z_C}{Z_C+R}V_{out}+\frac{R}{Z_C+R}V_{in}\cdots(2)$$
(1)式に(2)式を代入することで、$V_{out}$を求めることができます。
$$0=\frac{Z_C}{Z_C+R}V_{out}+\frac{R}{Z_C+R}V_{in}$$
$$\frac{Z_C}{Z_C+R}V_{out}=-\frac{R}{Z_C+R}V_{in}$$
$$V_{out}=-\frac{R}{Z_C}V_{in}$$
ここまでは反転増幅回路の計算と同じでしたが、さらに$Z_C$の部分を計算します。コンデンサのインピーダンス$\frac{1}{jωC}$を$Z_C$に代入すると以下のようになります。
$$V_{out}=-\frac{R}{\frac{1}{jωC}}V_{in}=-jωCRV_{in}\cdots(3)$$
$\frac{1}{jω}$は位相が90°遅れ、周波数が高くなるほど値が低くなることを表す複素数の虚部になります。複素数は三角関数または指数関数で表すことができ、オイラーの公式により以下のような関係があります。
$$e^{jθ}=cosθ+jsinθ$$
$θ[rad], ω[rad/s], t[s]$の関係は$θ=ωt$なので、オイラーの公式は以下のように表すこともできます。$$e^{jωt}=cosωt+jsinωt$$
また、底がネイピア数$e$である指数関数は微分・積分しても変化しない性質を持っています。
$$\frac{d}{dx}e^{x}=e^{x}$$
$$\int e^{x}dx=e^{x}$$
そのため、$e^{jωt}$を微分すると、以下のようになります。
$$\frac{d}{dt}e^{jωt}=jω\frac{d}{d(jωt)}e^{jωt}=jωe^{jωt}$$
つまり、微分と$jω$の関係は以下のようになることがわかります。
$$\frac{d}{dt}=jω$$
よって、$\frac{d}{dt}=jω$を(3)式に代入することで最終的な$V_{out}$は以下のようになります。
$$V_{out}=-jωCRV_{in}=-CR\frac{dV_{in}}{dt}$$
ヌラーモデルを使った計算
完全微分回路

これより、理想オペアンプをヌラーモデルに置き換えて、完全微分回路を以下の通り計算してみます。
ヌラーモデルを用いることで、オペアンプの仮想短絡(イマジナリショート/バーチャルショート)の状態などを表すことができるので、計算を簡単にできるのです。
なお、ヌラーモデル自体の詳しい解説は以下の記事をご覧ください。
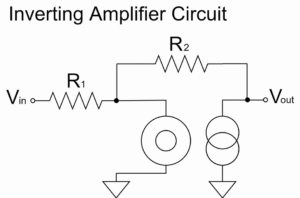
完全微分回路(ヌラーモデル)
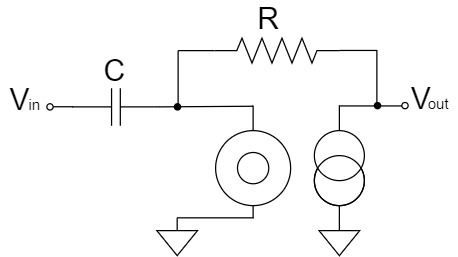
見やすくするために、回路図の形を変形させます。
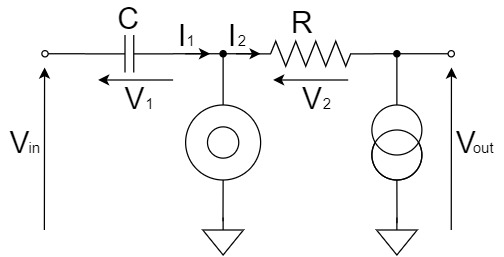
キルヒホッフの第1法則(電流則)より、$I_1$と$I_2$は以下の関係が成立します。
$$I_2=I_1$$
コンデンサの充電電流$I_1$は、コンデンサの端子電圧$V_1$の微分値とと$C$をかけた値になることから、以下のようになります。
$$I_1=C\frac{dV_1}{dt}=C\frac{dV_{in}}{dt}\cdots(1)$$
また、$I_2$は以下のようになります。
$$I_2=\frac{V_2}{R}=\frac{-V_{out}}{R}=-\frac{V_{out}}{R}\cdots(2)$$
(1)式と(2)式を$I_2=I_1$に代入すると、完全微分回路の関係式を求めることができます。
$$-\frac{V_{out}}{R}=C\frac{dV_{in}}{dt}$$
$$V_{out}=-CR\frac{dV_{in}}{dt}$$
このように、ヌラーモデルを用いた完全微分の等価回路から、関係式を算出することができました。
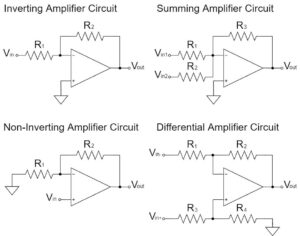
その他のオペアンプの回路例
当記事では、「オペアンプの積分回路」について詳しく解説してきましたが、その他にもオペアンプには様々な回路が存在します。
以下の記事で、比較的よく使われるオペアンプの回路について紹介しているので、ぜひご覧ください。