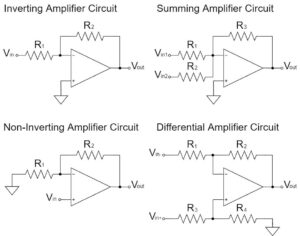
オペアンプの加算回路

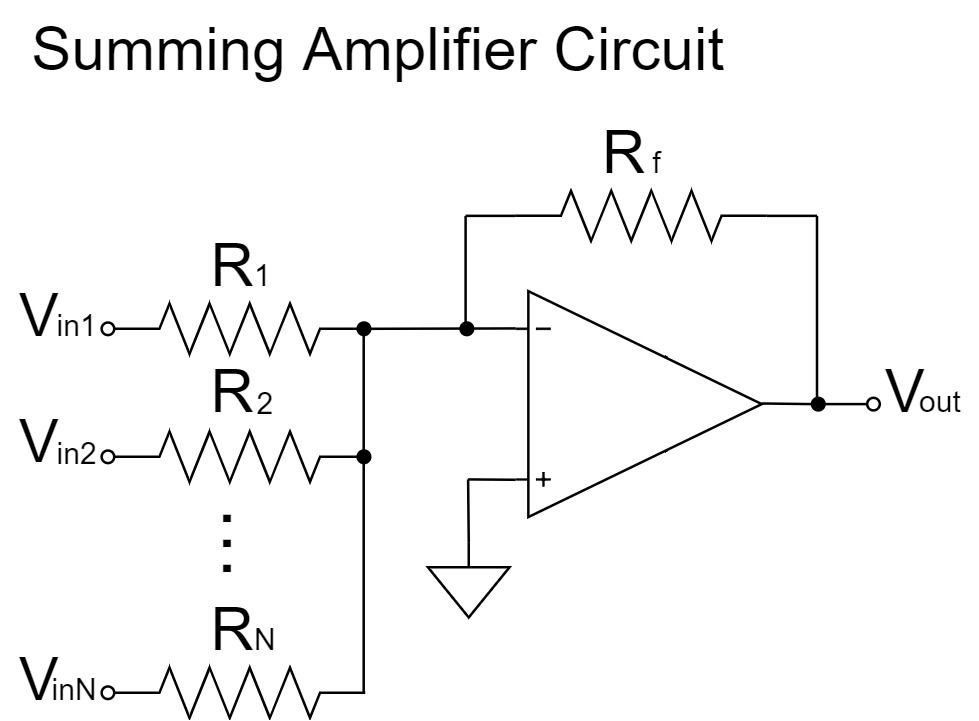
当記事では、「オペアンプ(OPアンプ/OP-Amp)の加算回路」について詳しく解説していきます。

加算回路は、オペアンプの反転増幅回路を応用して、複数の入力電圧を加算(足し算)して出力する回路です。

オペアンプの加算回路の特徴

加算回路

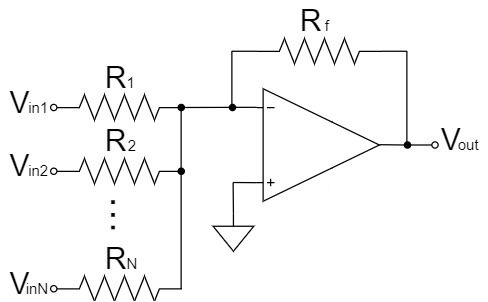
$$V_{out}=-\left(\frac{R_3}{R_1}V_{in1}+\frac{R_3}{R_2}V_{in2}+\cdots+\frac{R_f}{R_N}V_{inN}\right)$$
加算回路は、上式の通り、N個の入力電圧がある時、それぞれの$V_{inN}$の信号が増幅率$\frac{R_f}{R_N}$(重み付け)で増幅された総和が、$V_{out}$に出力されます。また、「$-$」の極性が表す通り、$V_{out}$の信号は反転されます。

抵抗比による重み付けが必要ない場合、$R_1=R_1=\cdots=R_N=R_f$であれば、以下のように出力電圧は単純に入力電圧の総和として簡単に計算できます。
$$V_{out}=-(V_{in1}+V_{in2}+\cdots+V_{inN})$$
例えば、$N=3,V_{in1}=2V,V_{in2}=3V,V_{in3}=5V$であれば、$V_{out}=-10V$になります。
$$V_{out}=-(V_{in1}+V_{in2}+V_{in3})=-(2+3+5)=-10[V]$$
また、$R_1=R_1=\cdots=R_N=R$、$R_f=R/N$であれば、平均値回路としてN個の入力電圧の平均値を求めることができます。
$$V_{out}=-\left(\frac{\frac{R}{N}}{R}V_{in1}+\frac{\frac{R}{N}}{R}V_{in2}+\cdots+\frac{\frac{R}{N}}{R}V_{inN}\right)$$
$$V_{out}=-\left(\frac{1}{N}V_{in1}+\frac{1}{N}V_{in2}+\cdots+\frac{1}{N}V_{inN}\right)$$
$$V_{out}=-\frac{V_{in1}+V_{in2}+\cdots+V_{inN}}{N}$$
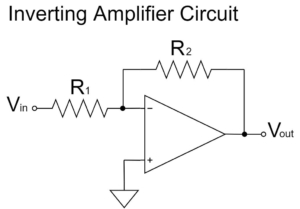
この加算回路は、反転増幅回路を応用したものなので、入力電圧が1個の時は、反転増幅回路の関係式になります。
$$V_{out}=-\left(\frac{R_f}{R_1}V_{in1}+\cancel{\frac{R_f}{R_2}V_{in2}}+\cdots+\cancel{\frac{R_f}{R_N}V_{inN}}\right)=-\frac{R_f}{R_1}V_{in1}$$
そのため、加算回路と反転増幅回路の主な特徴は共通しているので、先に反転増幅回路について理解しておいた方が良いでしょう。反転増幅回路の詳しい解説は以下の記事をご覧下さい。

オペアンプの加算回路の計算

オペアンプの加算回路の関係式を求めるために、理想オペアンプをヌラーモデルに置き換えた簡易計算をします。

加算回路

これより、理想オペアンプをヌラーモデルに置き換えて、加算回路を以下の通り計算してみます。

ヌラーモデルを用いることで、オペアンプの仮想短絡(イマジナリショート/バーチャルショート)の状態などを表すことができるので、計算を簡単にできるのです。

なお、ヌラーモデル自体の詳しい解説は以下の記事をご覧ください。

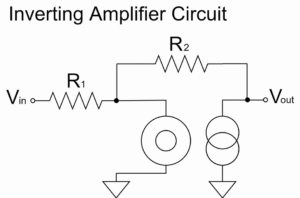
加算回路(ヌラーモデル)

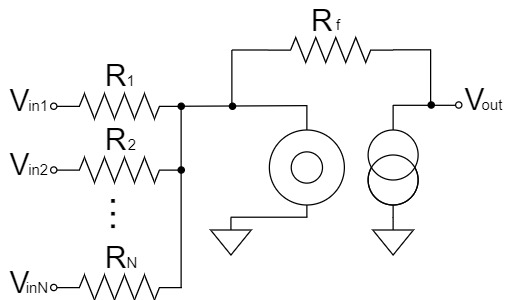
見やすくするために、回路図の形を変形させます。

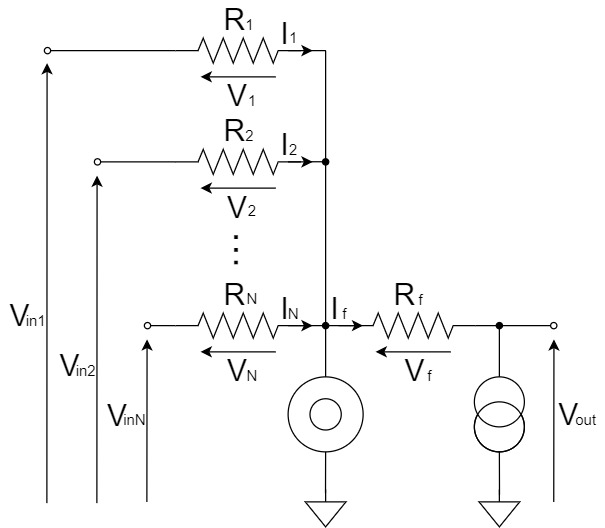
キルヒホッフの第1法則(電流則)より、$I_f,I_1,I_2,I_N$は以下の関係が成立します。
$$I_f=I_1+I_2+\cdots+I_N$$
また、$I_f,I_1,I_2,I_N$をそれぞれ求めると以下のようになります。
$$I_1=\frac{V_1}{R_1}=\frac{V_{in1}}{R_1} \qquad I_2=\frac{V_2}{R_2}=\frac{V_{in2}}{R_2} \qquad I_N=\frac{V_N}{R_N}=\frac{V_{inN}}{R_N}$$
$$I_f=\frac{V_f}{R_f}=\frac{-V_{out}}{R_f}=-\frac{V_{out}}{R_f}$$
(1)～(4)式を$I_f=I_1+I_2+\cdots+I_N$に代入すると、加算回路の関係式を求めることができます。
$$-\frac{V_{out}}{R_f}=\frac{V_{in1}}{R_1}+\frac{V_{in2}}{R_2}+\cdots+\frac{V_{inN}}{R_N}$$
$$V_{out}=-R_f\left(\frac{V_{in1}}{R_1}+\frac{V_{in2}}{R_2}+\cdots+\frac{V_{inN}}{R_N}\right)$$
$$V_{out}=-\left(\frac{R_f}{R_1}V_{in1}+\frac{R_f}{R_2}V_{in2}+\cdots+\frac{R_f}{R_N}V_{inN}\right)$$
このように、ヌラーモデルを用いた加算回路から、関係式を算出することができました。

出力信号が反転しない加算回路

今まで解説してきた加算回路は、反転増幅回路を応用した回路であるため、出力信号が反転してしまいます。

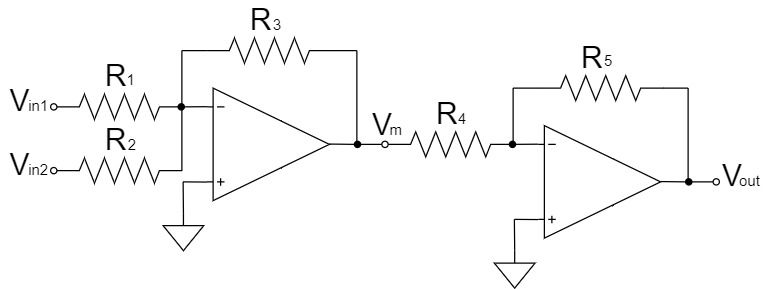
出力信号を反転しないようにするためには、上図のように加算回路の次に反転増幅回路を接続して、さらに反転させることで実現できます。

前段の加算回路の出力電圧$V_m$を計算すると以下のようになります。
$$V_m=-\left(\frac{R_3}{R_1}V_{in1}+\frac{R_3}{R_2}V_{in2}\right)$$
後段の反転増幅回路の出力電圧$V_{out}$は、入力電圧を$V_m$と考えれば良いので、以下のようになります。
$$V_{out}=-\frac{R_5}{R_4}V_m$$
$$V_{out}=\frac{R_5}{R_4}\left(\frac{R_3}{R_1}V_{in1}+\frac{R_3}{R_2}V_{in2}\right)$$
$R_4=R_5$とすれば、増幅率1倍の反転増幅となり、$R_1=R_2=R_3$とすれば単純な電圧の加算計算になるので、結果的に出力信号が反転しない加算回路になります。
$$V_{out}=V_{in1}+V_{in2}$$
この他にも、あまり一般的ではありませんが、非反転増幅回路を応用した加算回路で出力信号を反転しないようにすることが可能です。

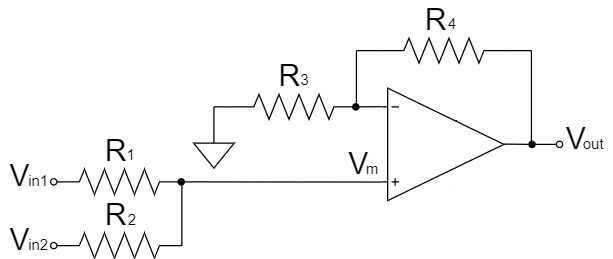
上図の加算回路は、2個の入力電圧を加算する回路となり、抵抗分圧による平均値回路と非反転増幅回路を組み合わせたものになります。

前段の抵抗分圧による平均値回路の出力電圧$V_m$を計算すると以下のようになります。
$$V_m=\frac{R_2V_{in1}+R_1V_{in2}}{R_1+R_2}$$
後段の非反転増幅回路の出力電圧$V_{out}$は、入力電圧を$V_m$と考えれば良いので、以下のようになります。
$$V_{out}=\left(1+\frac{R_4}{R_3}\right)V_m$$
$$V_{out}=\left(1+\frac{R_4}{R_3}\right)\left(\frac{R_2V_{in1}+R_1V_{in2}}{R_1+R_2}\right)$$
$R_3=R_4$とすれば、増幅率2倍の非反転増幅となり、$R_1=R_2$とすれば単純な平均値計算になるので、結果的に$V_{in1}$と$V_{in2}$を加算する関係式になります。
$$V_{out}=2\left(\frac{V_{in1}+V_{in2}}{2}\right)=V_{in1}+V_{in2}$$
ただし、非反転増幅回路を応用した加算回路は、入力電圧を印加している信号源が別々だと、信号源同士が干渉を起こして入力電圧が変動してしまいます。

反転増幅回路を応用した加算回路であれば、それぞれの信号源は、仮想短絡(イマジナリショート/バーチャルショート)を通じてGNDに接続(仮想接地)されていると考えることができるので、信号源同士が干渉することはありません。

また、今回は、例として2個入力の非反転増幅回路を応用した加算回路を挙げましたが、入力数を増やしていくと計算が複雑になるのも欠点です。

そのため、実用的な加算回路は、反転増幅回路を応用した回路を用いることがほとんどになります。

なお、非反転増幅回路の詳しい解説は以下の記事をご覧下さい。

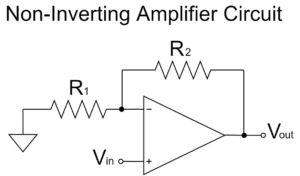
その他のオペアンプの回路例

当記事では、「オペアンプの加算回路」について詳しく解説してきましたが、その他にもオペアンプには様々な回路が存在します。

以下の記事で、比較的よく使われるオペアンプの回路について紹介しているので、ぜひご覧ください。