抵抗の仕様・特性

当記事では、抵抗の仕様・特性について詳しく解説します。

なお、当記事では主にKOA社のデータシート(RK73Hシリーズの角形チップ抵抗)に記載されている抵抗の仕様・特性を参考にさせていただきました。

KOA RK73Hシリーズの角形チップ抵抗は、一般的に電子回路によく使われる厚膜型金属皮膜抵抗になります。

抵抗の定格

以下のように、オペアンプの定格のパラメータを一覧形式で示します。

参考として、KOA RK73Hシリーズの角形チップ抵抗2A(2012)のパラメータも一緒に併記してあります。

定格/Rating

パラメータ		単位	形名:2A
定格電力	Power Rating	$W$	0.25$[W]$
定格周囲温度	Rated Ambient Temp.	$℃$	70$[℃]$
定格端子部温度	Rated Terminal Part Temp.	$℃$	125$[℃]$
抵抗温度係数	T.C.R.	$ppm/℃$	±100$[ppm/℃]$ ±200$[ppm/℃]$ ±400$[ppm/℃]$ ※抵抗値によって異なる
抵抗値範囲	Resistance Range	$Ω$	1$[Ω]$～10$[MΩ]$ ※F±1% E24/E96
最高使用電圧	Maximum Working Voltage	$V$	150$[V]$
最高過負荷電圧	Maximum Overload Voltage	$V$	200$[V]$
使用温度範囲	Operating Temperature Range	$℃$	-55～155$[℃]$
負荷軽減曲線	Derating Curve	-	-
温度上昇	Temperature Rise	-	-
ワンパルス限界曲線 (ワンパルス限界電力)	One-Pulse Limiting Electric Power	-	-

なお、以下のリンクから、KOA 面実装抵抗器のデータシートがダウンロードできるので、当記事と併せて読むことによって、より理解が深まると思います。

定格電力/Power Rating

定格電力は、抵抗の端子間に連続して加えることができる直流電圧または交流電圧(実効値)の最大値です。

以下のように、定格電力と抵抗値から、定格電圧を求めることができます。
$$定格電圧[V]=\sqrt{定格電力[W] \times 公称抵抗値[Ω]}$$
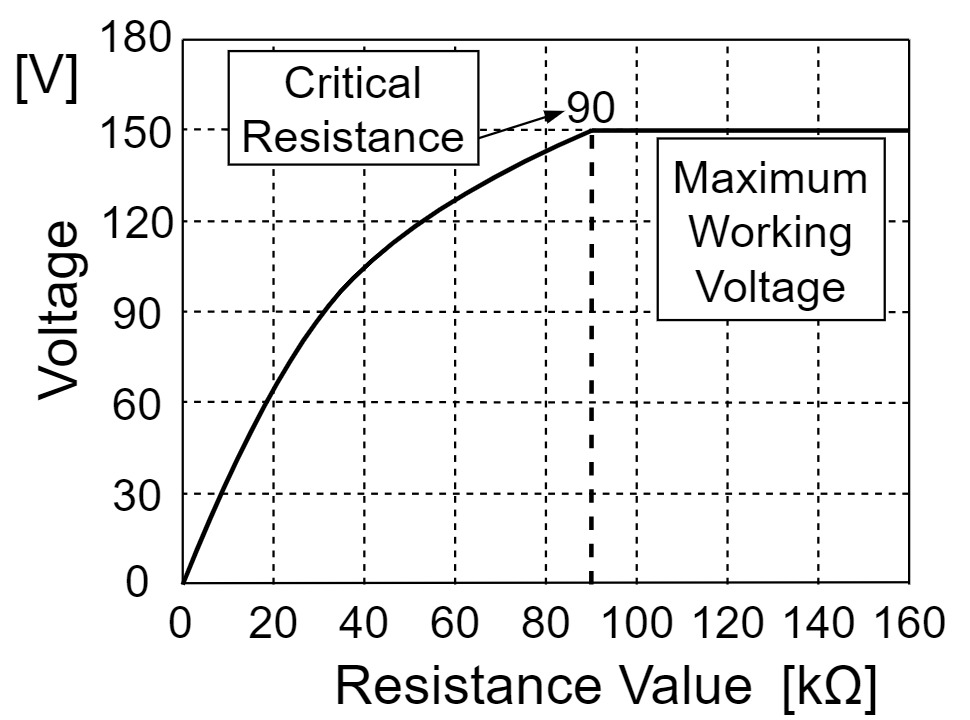
この式より、KOA RK73Hシリーズの角形チップ抵抗2Aにおいて、抵抗と定格電圧の関係をグラフにしたものが以下のようになります。

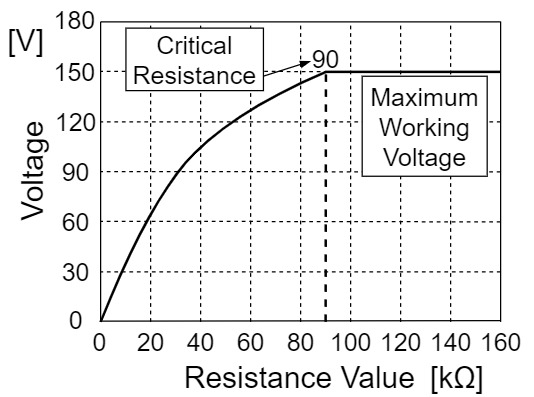
上記のグラフでは、抵抗値が増加するごとに、定格電圧も増加していますが、後ほど説明する最高使用電圧/Maximum Working Voltageの$150[V]$で一定になることがわかります。

また、定格電圧と最高使用電圧が一致する抵抗値を求めると以下のようになります。
$$臨海抵抗値(公称抵抗値)[Ω]=\frac{最高使用電圧(定格電圧)[V]^2}{定格電力[W]}=\frac{150^2}{0.25}=90[kΩ]$$
この抵抗値を臨海抵抗値/Critical Resistanceと言います。

つまり、臨界抵抗値以下では、抵抗に加えられる最高使用電圧は定格電圧と同じと言うことになります。

定格周囲温度/Rated Ambient Temp.

定格周囲温度は、定格電力での抵抗周囲の最高温度です。

あくまで「抵抗周囲」になるので、機器内部に抵抗が実装された基板が組み込まれている場合、機器外部の周囲温度ではなく、機器内部の周囲温度になります。

定格端子部温度/Rated Terminal Part Temp.

定格端子部温度は、定格電力での抵抗端子部の最高温度です。自己発熱による温度上昇分も含みます。

抵抗温度係数/T.C.R.

抵抗温度係数は、温度による抵抗値の変化の度合いです。単位は$[ppm(10^{-6})/℃]$で表します。
抵抗温度係数の関係式は以下のようになります。
$$抵抗温度係数[ppm/℃]=\frac{R-R_0}{R_0} \times \frac{1}{T-T_0} \times 10^6$$

• $R:T[℃]における抵抗値[Ω]$
• $R_0:T_0[℃]における抵抗値[Ω]$
• $T:試験温度[℃]$
• $T_0:基準温度[℃]$

例えば、KOA RK73Hシリーズの角形チップ抵抗2Aの場合、$10～1[MΩ]$の抵抗値範囲では、$±100[ppm/℃]$になります。

なぜ、±になっているかと言うと、以下のように温度による抵抗値変化率をグラフ(赤:+100[ppm/℃]、赤:-100[ppm/℃])にしてみると、部品の個体により抵抗が温度に対して比例または反比例して変化するからです。

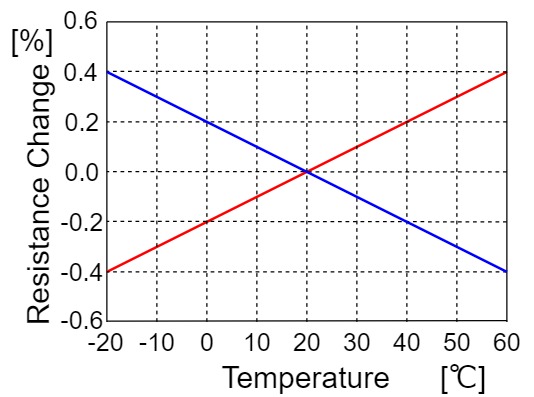
仮に、$20℃$で$100[kΩ]$の抵抗は、抵抗温度係数$α=+100[ppm/℃]$だとすると、50℃での抵抗値を以下のように求めることができます。
$$\frac{R-R_0}{R_0}=α \times 10^{-6} \times (T-T_0)$$
$$R-R_0=R_0 \times α \times 10^{-6} \times (T-T_0)$$
$$R=R_0+R_0 \times α \times 10^{-6} \times (T-T_0)$$
$$R=R_0\{1+α \times 10^{-6} \times (T-T_0)\}$$
$$R=100 \times 10^3 \times \{1+100 \times 10^{-6} \times (50-20)\}$$
$$R=100 \times 10^3 \times (1+3 \times 10^{-3})=100.3 \times 10^3=100.3[kΩ]$$
これにより、$20℃$で$100[kΩ]$の抵抗は、$50℃$になると抵抗値が$0.3[kΩ]$増加して$100.4[kΩ]$になることがわかります。

抵抗値範囲/Resistance Range

抵抗値範囲は、その名の通り、メーカーで用意している抵抗の範囲です。

例えば、KOA RK73Hシリーズの角形チップ抵抗2Aにおいて、抵抗値許容差F±1%の場合、E24またはE96系列で$1～10M[Ω]$の抵抗が用意されていることになります。

最高使用電圧/Maximum Working Voltage

最高使用電圧は、抵抗の端子間にに連続して加えることのできる直流電圧または交流電圧(実効値)の最高値になります。

先程、「定格電力」で説明したように、臨界抵抗値以下で加えられる最高使用電圧は定格電圧と同じになります。

最高過負荷電圧/Maximum Overload Voltage

過負荷電圧は、過負荷試験(JIS C 5201-1 4.13)において5秒間、印加可能な直流電圧または交流電圧(実効値)です。

通常、定格電圧×2.5(保証倍率)で過負荷試験を行いますが、高抵抗になると、過電圧になってしまい抵抗を破壊してしまいます。

そのため、定格電圧と最高使用電圧/Maximum Working Voltageの関係のように、ある抵抗値(臨海抵抗値/Critical Resistance)を超えた後、過負荷電圧は一定となります。

この過負荷試験に使用できる一定となった上限電圧が、最高過負荷電圧となります。

KOA RK73Hシリーズの角形チップ抵抗2Aにおいて、抵抗と過負荷電圧の関係をグラフにしたものが以下のようになります。

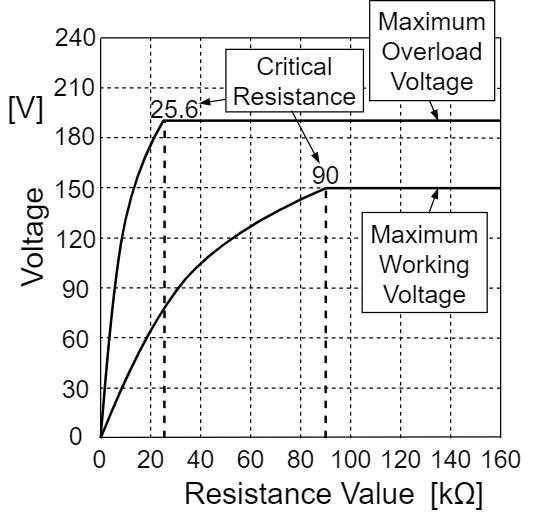
上記のグラフでは、抵抗値が増加するごとに、過負荷電圧も増加していますが、最高過負荷電圧の$200[V]$で一定になることがわかります。

また、過負荷電圧と最高過負荷電圧が一致する臨海抵抗値を求めると以下のようになります。
$$定格電圧[V]=\sqrt{定格電力[W] \times 公称抵抗値[Ω]}$$
$$\frac{最高過負荷電圧[V]}{2.5}=\sqrt{定格電力[W] \times 臨海抵抗値[Ω]}$$
$$\left(\frac{最高過負荷電圧[V]}{2.5}\right)^2=定格電力[W] \times 臨海抵抗値[Ω]$$
$$臨海抵抗値[Ω]=\frac{\left(\frac{最高過負荷電圧[V]}{2.5}\right)^2}{定格電力[W]}$$
$$臨海抵抗値[Ω]=\frac{\left(\frac{200}{2.5}\right)^2}{0.25}=25600=25.6[kΩ]$$
これにより、最高過負荷電圧が$200[V]$の場合、臨海抵抗値は$25.6[kΩ]$になることがわかります。

使用温度範囲/Operating Temperature Range

使用温度範囲は、抵抗に電圧が加わっていて動作させている時に壊れない空気中の周囲温度範囲です。

負荷軽減曲線/Derating Curve

負荷軽減曲線は、周囲温度または端子部温度によって、定格電力に対して、どのぐらいの割合で電力を連続して加えることができるのかを示しています。

抵抗の定格電力に対する使用率は、定格電力比/Percent rated power(または負荷率、ディレーティング)と言います。

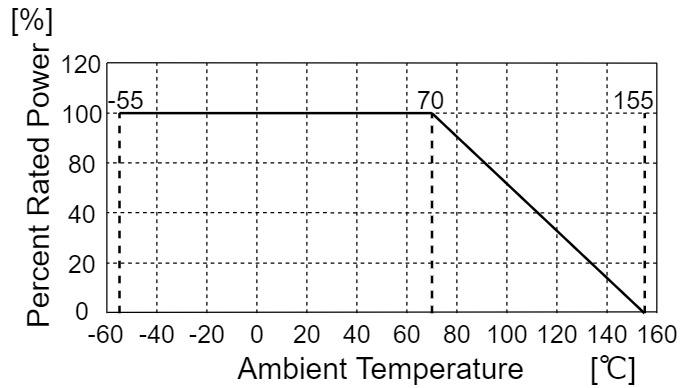
KOA RK73Hシリーズの角形チップ抵抗2Aの場合、周囲温度の負荷軽減曲線を見ると、$70[℃]$までは定格電力の$100$[%]ですが、$70[℃]$を超えると、定格電力比が段々と減少していくのがわかります。

例えば、$120[℃]$だと、定格電力の$40$[%]しか加えることができないことになります。

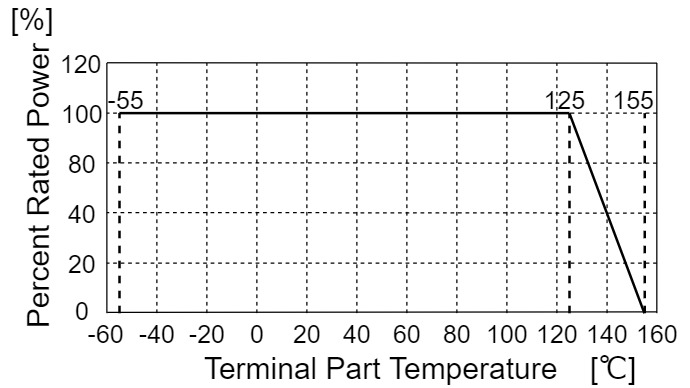
一方、端子部温度の負荷軽減曲線を見ると、$125[℃]$までは定格電力の$100$[%]ですが、$125[℃]$を超えると、定格電力比が段々と減少していくのがわかります。

端子部温度は、周囲温度より高音になるため、定格電力比の減少が始まる温度も端子部温度の方が高くなります。

ただし、周囲温度は$70[℃]$、端子部温度は$125[℃]$までは、定格電力の$100$[%]ギリギリまで使って良いわけではありません。

定格電力比が高くなると、それだけ抵抗の温度が上昇して故障率が高くなってしまいます。

そのため、抵抗の種類などによって違いますが、目安として定格電力比を$25～50$[%]程度で使用すると良いでしょう。

温度上昇/Temperature Rise

温度上昇は、抵抗に電流が流れて電圧が加わった時、抵抗の温度がどのぐらい上昇するのかを示しています。

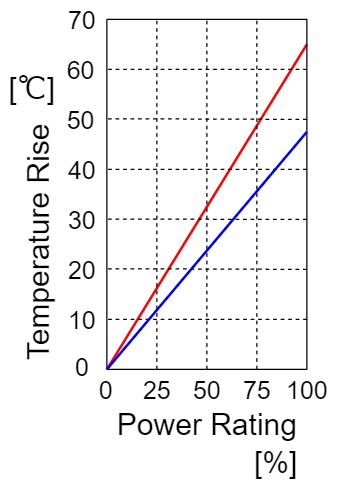
KOA RK73Hシリーズの角形チップ抵抗2Aの場合、以下のように定格電力比(または負荷率、ディレーティング)と温度上昇の関係を(赤:抵抗表面中央/Hot spot、青:抵抗端子部/Terminal)にしてみると、定格電力比に対して温度が比例して上昇しています。

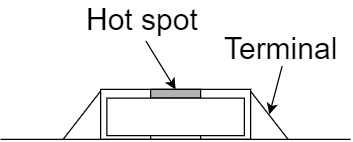
例えば、定格電力比が50[%]の場合、抵抗表面中央/Hot spotの温度は約33[℃]、抵抗端子部/Terminalの温度は約24[℃]上昇することになります。

抵抗の温度が上昇し過ぎてしまうと、故障率が高まったり、抵抗の周りの熱に弱い電子部品が影響を受けてしまうので、「負荷軽減曲線」で説明した通り、定格電力比を$25～50$[%]程度で使用すると良いでしょう。

その他、抵抗を実装する基板のランドやパターンを大きめに取ったり、基板を取り付けるケース・シャーシに放熱穴やファンを配置することで、熱対策を行うことができます。

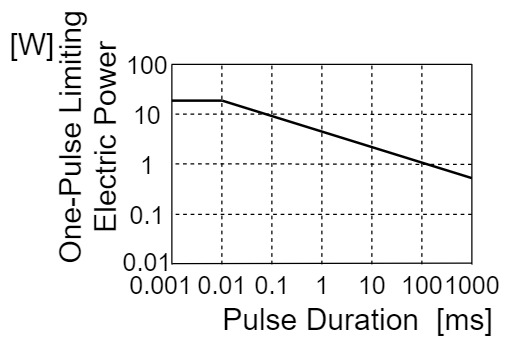
ワンパルス限界曲線(ワンパルス限界電力)/One-Pulse Limiting Electric Power

ワンパルス限界曲線(ワンパルス限界電力)は、雷サージや静電気など定格電力を超える瞬間的に高い電力が抵抗に加わった場合、どのぐらい耐えられるのかを示しています。

波形条件(ワンパルス)

例えば、KOA RK73Hシリーズの角形チップ抵抗2Aだと、パルス印加時間が$0.01[ms]$の場合、ワンパルス限界電力は$11[W]$になります。
(本来、ワンパルス限界曲線は対数グラフでデータシートの記載されていますが、当記事では目盛りを簡略化しています。)

そして、パルス印加時間が$0.01[ms]$を超えると、ワンパルス限界電力が段々と減少していくことがわかります。

ただし、データシートに記載されているワンパルス限界曲線は、保証値ではなく、あくまで参考値なので、実機で確認しなければなりません。

また、パルス波以外の正弦波や三角波などの波形は、パルス波に近似して考える必要があります。

抵抗の性能

以下のように、KOA RK73Hシリーズの角形チップ抵抗2A(2012)の性能を一覧形式で示します。

性能/Performance Characteristics

試験項目		規格値 (形式:2A) -保証値	規格値 (形式:2A) -代表値	試験方法
抵抗値	Resistance	規定の 許容誤差内	-	25℃
抵抗温度係数	T.C.R.	規定値内	-	+25℃/-55℃ +25℃/+125℃
過負荷(短時間)	Overload (Short time)	±2%	±0.5%	定格電圧×2.5倍を5秒印加
はんだ耐熱性	Resistance to Soldering Heat			260±5℃で10±1秒
温度急変	Rapid Change of Temperature	±0.5%	±0.3%	-55℃(30分)と+125℃(30分)を100回
耐湿負荷	Moisture Resistance	±2%	±0.75%	40±2℃と90～95%RHを1000時間 (1.5時間ON/0.5時間OFFの周期)
70℃または 定格端子部温度 での耐久性	Endurance at 70℃	±2%	±0.75%	70±2℃または 定格端子部温度±2℃を1000時間 (1.5時間ON/0.5時間OFFの周期)
高温放置	High Temperature Exposure	±1%	±0.3%	+155℃を1000時間

規格値は上記のような試験を行い、どの程度の誤差内なのかを示しています。保証値と代表値の違いについては、以下の通りになります。