オペアンプの電気的特性

当記事では、オペアンプ(OPアンプ/OP-Amp)の電気的特性について詳しく解説します。

なお、デバイスメーカー各社で、記載されている電気的特性が微妙に異なりますが、当記事では主にアナログ・デバイセズ社のデータシートに記載されている電気的特性のパラメータを参考にさせていただきました。

オペアンプの電気的特性とは何か？

オペアンプの電気的特性とは、オペアンプの実際の性能を示す仕様になります。

実物のオペアンプは理想オペアンプとは違い、様々な誤差を含んでいるので、いい加減にオペアンプを選ぶわけにはいきません。

設計する電子回路に最適なオペアンプを選定するためには、データシートを読み込んで事前にオペアンプの電気的特性について理解しておく必要があります。

なお、オペアンプの電気的特性を理解するには、事前に理想オペアンプについて知っておいた方が良いです。以下の記事で詳しく説明しているので、ぜひご覧ください。

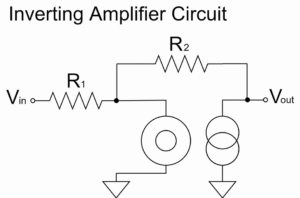
オペアンプの絶対最大定格の詳しい解説については、以下の記事をご覧ください。

オペアンプの電気的特性

以下のように、オペアンプの電気的特性のパラメータを一覧形式で示します。

アナログ・デバイセズ社など外資系デバイスメーカーのデータシートは必ず英語が最新になるので、併記してあるパラメータの英語名も覚えておくことをおすすめします。

電気的特性/ELECTRICAL SPECIFICATIONS

パラメータ		DC誤差	AC誤差	DC/AC誤差	記号	単位
入力オフセット電圧	Input Offset Voltage				$V_{OS}$	$V$
入力オフセット電圧ドリフト	Input Offset Voltage Drift				$ΔV_{OS}/ΔT$	$V/℃$
入力バイアス電流	Input Bias Current				$I_B$	$A$
入力バイアス電流ドリフト	Input Bias Current Drift				$ΔI_B/ΔT$	$I/℃$
入力オフセット電流	Input Offset Current				$I_{OS}$	$A$
同相入力電圧範囲	Common-Mode Input Voltage Range				-	$V$
同相除去比	Common-Mode Rejection Ratio				$CMRR$	$dB$, $V/V$
開放電圧利得	Open-loop Voltage Gain				$A_{OL}$	$dB$, $V/V$
出力電圧範囲	Output Voltage Range				-	$V$
電源除去比	Power Supply Rejection Ratio				$PSRR$	$dB$, $V/V$
静止消費電流 (アンプ当たり)	Quiescent Current per amplifier				$I_Q$	$A$
入力インピーダンス	Input Impedance				$Z_{IN}$	$Ω$
出力インピーダンス	Output Impedance				$Z_{OUT}$	$Ω$
周波数特性	Frequency Response				-	-
利得帯域幅積 (GB積)	Gain Bandwidth Product				$GBP$	$Hz$
位相余裕	Phase Margin				-	$deg$
ゲイン余裕	Gain Margin				-	$dB$
スルー・レート	Slew Rate				$SR$	$V/sec$
セトリング・タイム	Settling Time				$t_s$	$sec$
ノイズ	Noise				-	-
入力電圧ノイズ	Input Voltage Noise				$e_{n}p-p$	$V_{p-p}$
入力電圧ノイズ密度	Input Voltage Noise Density				$e_n$	$V/\sqrt{Hz}$
入力電流ノイズ密度	Input Current Noise Density				$i_n$	$A/\sqrt{Hz}$

※パラメータに対して、関連のある「DC誤差」、「AC誤差」、「DC/AC誤差」にそれぞれ○(関連度「高」)または△(関連度「中」)を示してあります。

入力オフセット電圧/Input Offset Voltage

入力オフセット電圧$V_{OS}$は、入力端子+(Input +)と入力端子-(Input -)の間に発生する電圧のズレのことを言います。

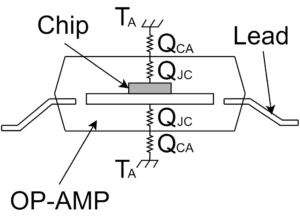
上図のように理想オペアンプの非反転増幅回路にオフセット電圧$V_{OS}$を加えたモデルと考えるとわかりやすいと思います。

以下のように、$V_{out}$を計算してみると、オフセット電圧$V_{OS}$の分だけの誤差が加わった値になります。
$$V_{out}=\left(1+\frac{R_2}{R_1}\right)V_{in}+\left(1+\frac{R_2}{R_1}\right)V_{OS}[V]$$
そのため、利得を高くするほど、誤差としてのオフセット電圧$V_{OS}$の影響が大きくなります。

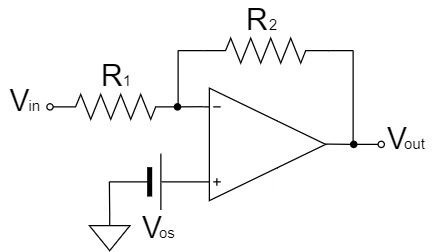
なお、反転増幅回路でも同じことが言え、オフセット電圧$V_{OS}$が加わった出力電圧を求めると以下のようになります。
$$V_{out}=\left(-\frac{R_2}{R_1}\right)V_{in}+\left(1+\frac{R_2}{R_1}\right)V_{OS}[V]$$

入力オフセット電圧ドリフト/Input Offset Voltage Drift

入力オフセット電圧ドリフト$ΔV_{os}/ΔT$は、入力オフセット電圧$V_{os}$の温度ドリフト(温度係数)のことで、温度変動による入力オフセット電圧$V_{os}$の変化を示します。

入力バイアス電流/Input Bias Current

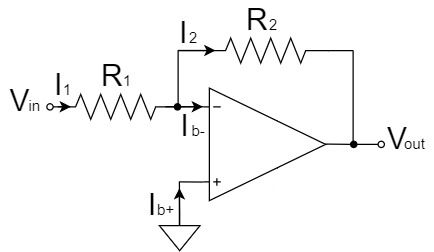
入力バイアス電流$I_{B}$は、オペアンプの入力端子+(Input +)と入力端子-(Input -)にそれぞれ流れ込む電流のことを言います。

理想オペアンプは入力バイアス電流$I_{B}$は0なのですが、実物のオペアンプでは入力バイアス電流$I_{B}$がフィードバック抵抗に流れ込むことによりオフセット電圧が発生します。
(このオフセット電圧は、先程説明した「入力オフセット電圧」とは違ったパラメータですので混同しないように注意して下さい。)

例えば、反転増幅回路で、入力バイアス電流$I_{B}$によるオフセット電圧を計算すると以下のようになります。
$$I_1=\frac{V_{in}}{R_1}[A]$$
$$I_2=I_1-I_{B-}=\frac{V_{in}}{R_1}-I_{B-}[A]$$
$$V_{out}=-R_2I_2=-\frac{R_2}{R_1}V_{in}+R_2I_{B-}[V]$$
このことから、$R_2I_{B-}$のオフセット電圧が誤差要因となり、フィードバック抵抗$R_2$の値が大きいほど影響が大きくなることがわかります。

反転増幅回路であれば、反対側の入力端子+(Input +)に抵抗(バイアス補償抵抗)を直列に接続してオフセット電圧を発生させることで、バイアス電流$I_{B}$をキャンセルすることもできます。

しかし、$I_{B+}$と$I_{B-}$は全く同じ値ではないため、その差分が「入力オフセット電流$I_{OS}$」となります。

入力バイアス電流ドリフト/Input Bias Current Drift

入力バイアス電流ドリフト$ΔI_{B}/ΔT$は、入力バイアス電流の温度ドリフト(温度係数)のことで、温度変動による入力バイアス電流の変化を示します。

入力オフセット電流/Input Offset Current

「入力バイアス電流」で説明した通り、バイアス電流の$I_{B+}$と$I_{B-}$は全く同じ値ではないため、バイアス電流$I_{B}$をキャンセルしたとしても、その差分が「入力オフセット電流$I_{OS}$」となります。

そして、入力バイアス電流$I_{B}$より小さくなりますが、入力オフセット電流$I_{OS}$がオペアンプのフィードバック抵抗に流れることにより、オフセット電圧が発生し誤差要因となります。

反転増幅回路の場合、以下のように計算できます。
$$I_{OS}=|I_{B+}-I_{B-}|[A]$$
$$V_{out}=-\frac{R_2}{R_1}V_{in}+R_2I_{OS}[V]$$

同相入力電圧範囲/Common-Mode Input Voltage Range

同相入力電圧範囲は、オペアンプに入力できる電圧の範囲のことを言います。単に「入力電圧範囲/Input Voltage Range」とデータシートに記載されている場合もあります。

特にオペアンプの電源電圧の範囲一杯まで入力または出力できる場合、レール・トゥ・レール・オペアンプ(Rail to Rail OP-AMP)と呼びます。

例えば、オペアンプの電源が±15Vとすると、レール・トゥ・レール・オペアンプだと、電源と同じく±15Vまで入力または出力できることになります。

ただ、「入出力ともにレール・トゥ・レール」、「出力のみレール・トゥ・レール」などとオペアンプによって異なるので、データシートで「出力電圧範囲」もしっかり確認しておいて下さい。

同相除去比/Common-Mode Rejection Ratio

同相除去比CMRRは、オペアンプの入力端子に入力されている同相電圧に変動(リップル)がある時に、その変動を除去できる能力のことを言います。特に差動増幅回路(減算回路)において重要なパラメータです。

オペアンプの同相入力電圧の変動を$ΔV_{CM}$、オペアンプの入力オフセット電圧の変動を$ΔV_{OS}$とすると、以下のように定義することができます。
$$CMRR=\frac{ΔV_{CM}}{ΔV_{OS}}[V/V] \quad or \quad CMRR=20log\frac{ΔV_{CM}}{ΔV_{OS}}[dB]$$
この関係式から、同相入力電圧の変動に対して、入力オフセット電圧の変動が小さいほど同相除去比CMRRが大きくなることがわかります。

また、オペアンプの差動電圧利得を$A_d$、オペアンプの同相電圧利得を$A_c$とすると、以下のように定義することもできます。
$$CMRR=\frac{A_d}{A_c}[V/V] \quad or \quad CMRR=20log\frac{A_d}{A_c}[dB]$$
こちらの関係式からは、差動電圧利得に比べて同相電圧利得が小さいほど同相除去比CMRRが大きくなることがわかります。

そのため、同相除去比CMRRが大きければ、オペアンプの差動増幅回路において、コモンモードノイズを除去することができます。

ただし、差動増幅回路の抵抗の誤差により、同相除去比CMRRの値に影響を与えてしまうので注意する必要があります。

この点の詳しい解説については別記事にて行う予定です。

開放電圧利得/Open-loop Voltage Gain

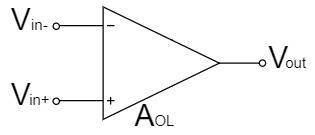
開放電圧利得(オープンループ電圧利得)$A_{OL}$は、上図のように負帰還がない状態(開放時)で直流の差動電圧$V_{in+}-V_{in-}$をオペアンプに加えた時の利得です。
(1V以上の大信号を加えることから、大信号電圧利得$A_{VO}$/Large Signal Voltage Gain $A_{VO}$とデータシートに記載されている場合もあります。)

開放電圧利得$A_{OL}$は以下のように求めることができます。
$$A_{OL}=\frac{V_{out}}{V_{in+}-V_{in-}}[V/V] \quad or \quad A_{OL}=20log\frac{V_{out}}{V_{in+}-V_{in-}}[dB]$$

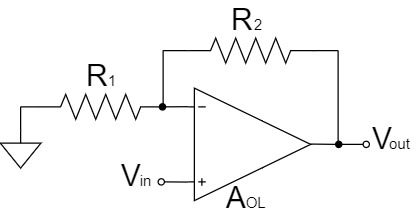
ここで、例として非反転増幅回路の増幅率に開放電圧利得がどのように影響するのか考えてみたいと思います。
$$V_{out}=\left(1+\frac{R_2}{R_1}\right)V_{in} \times \frac{1}{1+\left(1+\frac{R_2}{R_1}\right)\frac{1}{A_{OL}}}[V]$$
理想オペアンプの場合、開放電圧利得は$A_{OL}=∞$となるので、当然ながら非反転増幅回路の増幅率に影響はありません。
$$V_{out}=\left(1+\frac{R_2}{R_1}\right)V_{in} \times \frac{1}{1+\left(1+\frac{R_2}{R_1}\right)\frac{1}{∞}}=\left(1+\frac{R_2}{R_1}\right)V_{in}[V]$$
しかし、実物のオペアンプの開放電圧利得は有限です。$R_1=1[kΩ]$、$R_1=10[kΩ]$、$A_{OL}=80[dB](10000倍)$で計算すると、非反転増幅回路で得られる増幅率は以下のようになります。
$$V_{out}=(11)V_{in} \times \frac{1}{1+(11)\frac{1}{10000}}=\frac{11}{1.0011}V_{in}≒10.988V_{in}$$
理想オペアンプの非反転増幅回路で得られる増幅率11倍より小さくなっており、その差を「利得誤差」と言います。

出力電圧範囲/Output Voltage Range

出力電圧範囲は、オペアンプが出力できる電圧の範囲のことを言います。「出力電圧ハイレベル/Output Voltage High」、「出力電圧ローレベル/Output Voltage Low」とデータシートに記載されている場合もあります。

「同相入力電圧範囲」で説明した通り、オペアンプの電源電圧の範囲一杯まで入力または出力できる場合、レール・トゥ・レール・オペアンプ(Rail to Rail OP-AMP)と呼びます。

ただ、「入出力ともにレール・トゥ・レール」、「出力のみレール・トゥ・レール」などとオペアンプによって異なるので、データシートで「同相入力電圧範囲」もしっかり確認しておいて下さい。

電源除去比/Power Supply Rejection Ratio

電源除去比PSRRは、オペアンプの電源端子に入力されている電圧に変動(リップル)がある時に、その変動を除去できる能力のことを言います。

オペアンプの電源電圧の変動を$ΔV_S$、オペアンプの入力オフセット電圧の変動を$ΔV_{OS}$とすると、以下のように定義することができます。
$$PSRR=\frac{ΔV_S}{ΔV_{OS}}[V/V] \quad or \quad PSRR=20log\frac{ΔV_S}{ΔV_{OS}}[dB]$$
例えば、$PSRR=100[dB]=10^5[倍]$、$ΔV_S=10[V]$とすると、以下のように$ΔV_{OS}$を算出できます。
$$ΔV_{OS}=\frac{ΔV_S}{PSRR}=\frac{10}{10^5}=10[uV]$$
つまり、オペアンプで100倍増幅すると、出力電圧が$1[mV]$変動することになります。

静止消費電流(アンプ当たり)/Quiescent Current per amplifier

静止消費電流は、オペアンプに電源のみが加わっているだけで、入力信号や負荷電流も流れていない状態(静止状態)で、オペアンプが消費する電流のことを言います。

データシートには、静止消費電流は「アンプ当たり」で記載されていることが多いです。

入力インピーダンス/Input Impedance

実物のオペアンプの入力インピーダンスは、$10^{6}[Ω]$～$10^{9}[Ω]$オーダになっています。
(理想オペアンプは$∞[Ω]$)

非反転増幅回路の入力インピーダンスは、オペアンプの入力インピーダンスとほぼ等しくなりますが、反転増幅回路の入力インピーダンスは、入力端子-(Input -)に接続されている入力抵抗の値になります。

ただし、非反転増幅回路でも、入力端子+(Input +)とGNDに抵抗を接続することで任意の入力インピーダンスを設定することが可能です。

出力インピーダンス/Output Impedance

実物のオペアンプの出力インピーダンスは、$10^{2}[Ω]$オーダになっています。
(理想オペアンプは$0[Ω]$)

ただし、反転増幅回路や非反転増幅回路のように負帰還がある回路の場合、出力インピーダンスで生じる電圧降下は補償されるため、出力インピーダンスをほぼ$0[Ω]$として考えることもできます。

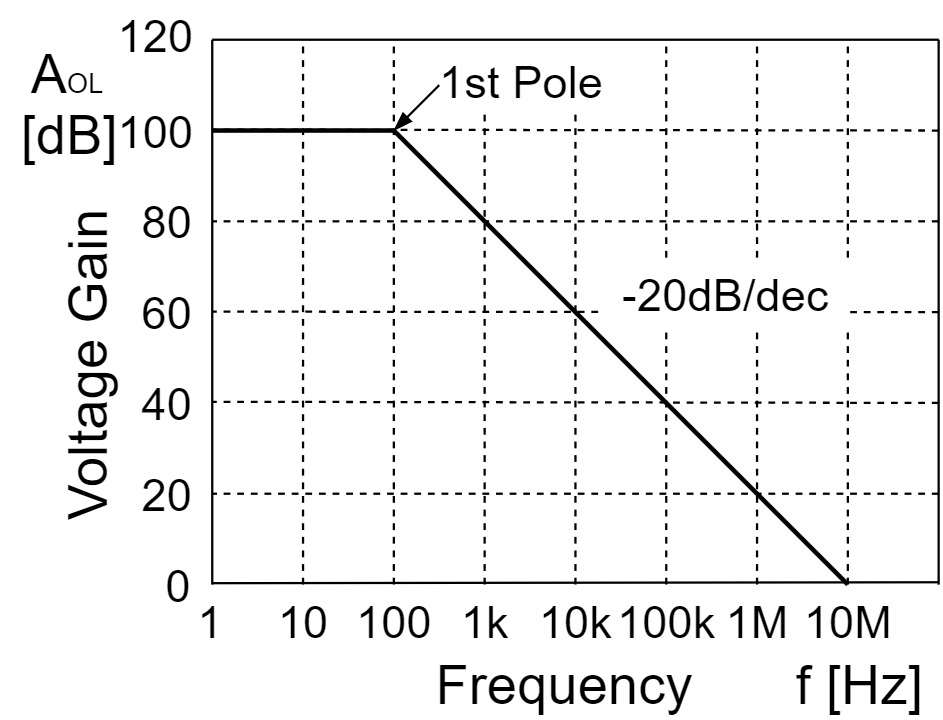
周波数特性/Frequency Response

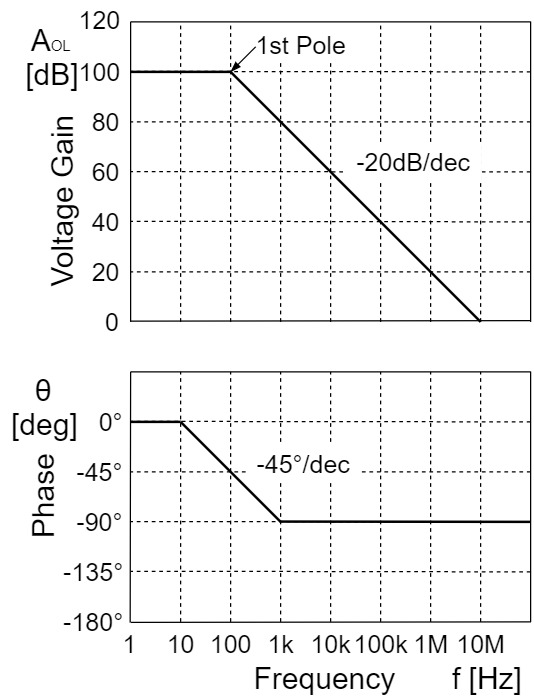
オペアンプの周波数特性は、一般的に「開放電圧利得$A_{OL}$(オープンループ電圧利得$A_{OL}$)」と「位相$θ$」の周波数特性を指します。

理想オペアンプでは、全周波数帯域で利得は一定になりますが、実物のオペアンプでは、ある周波数から利得が$-20[dB/dec](-6[dB/oct])$の傾きで減少していきます。

この利得が下がり始める周波数のことを「ポール(極)」、利得が$0[dB]$(1倍)になる「周波数を単一利得周波数$f_T$(ユニティゲイン周波数$f_T$)」と言います。

一方、位相については、ポールの1/10倍の周波数から遅れ始め、ポールの周波数で$-45°$、ポールの10倍の周波数で$-90°$になった後、一定になります。

また、上図のような周波数特性は完全補償型のオペアンプになりますが、非補償型型のオペアンプだと、以下のように1stポールと2ndポールの2つのポールが存在する周波数特性になります。

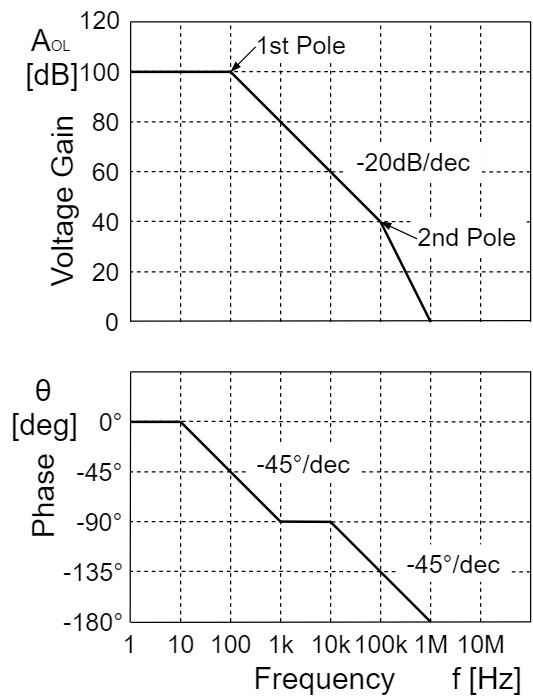
この場合、2ndポールで、利得の減衰量が$-40[dB/dec](-12[dB/oct])$となり、位相はさらに2ndポールの周波数で$-45°$、ポールの10倍の周波数で$-90°$に遅れます。そのため、位相遅れは最大で$-180°$に到達します。

オペアンプの位相が$-180°$遅れると、本来の負帰還が反転して正帰還に変わってしまうため発振してしまいます。

完全補償型のオペアンプの場合、位相遅れが$-90°$で一定になるので通常、発振しませんが、オペアンプの反転入力や出力にコンデンサなどの容量成分が接続されると、CR積分回路による位相遅れが生じて発振する可能性が高くなります。

※ポールの周波数で、1次のローパスフィルタのように$-3[dB/dec]$減衰しますが、当記事の周波数特性の図では省略してあります。

利得帯域幅積(GB積)/Gain Bandwidth Product(GBW)

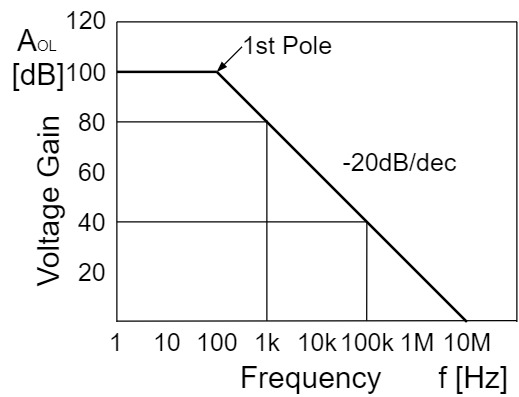
利得帯域幅積(GB積)$GBW$は、完全補償型のオペアンプの場合、$-20[dB/dec]$で減衰する領域において、任意の周波数と増幅率の積のことを言います。

周波数$f[Hz]$、増幅率$A[倍]$とすると、利得帯域幅積(GB積)$GBW$は以下のような式になります。
$$GBW=fA[Hz]$$
例として、$f=1[kHz]$、$A=80[dB]=10000[倍]$の時の$GBW_1$と$f=100[kHz]$、$A=80[dB]=100[倍]$の$GBW_2$をそれぞれ求めると、以下のようになります。
$$GBW_1=fA=1\times10^3\times10000=10\times10^6=10[MHz]$$
$$GBW_2=fA=100\times10^3\times100=10\times10^6=10[MHz]$$
$$GBW_1=GBW_2$$
このことから、$-20[dB/dec]$で減衰する領域において、常に利得帯域幅積(GB積)$GBW$は一定になることがわかります。

そのため、利得帯域幅積(GB積)$GBW$が大きいオペアンプほど、より高い周波数帯域まで安定して増幅することができることを表します。

位相余裕/Phase Margin

位相余裕は、利得(ゲイン)が$0[dB]$の周波数において、位相が$-180°$からどのぐらい余裕があるのかを示しています。

通常のオペアンプでは、位相が$45～60°$程度で設計されており、ゲイン余裕と同様に発振の余裕度として使われます。

例として、以下の図では位相余裕が$90°$のため、十分に位相余裕があり、通常の使い方では発振しません。

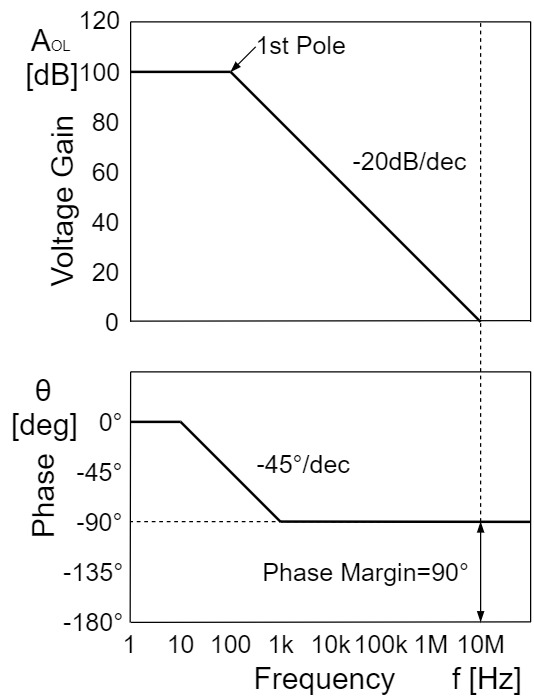
また、以下の図では位相余裕が$0°$のため、本来の負帰還が反転して正帰還となり発振してしまいます。

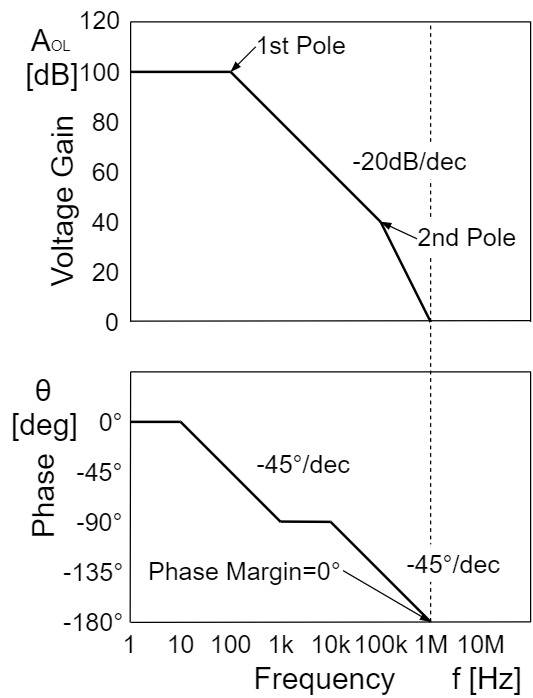
ゲイン余裕/Gain Margin

ゲイン余裕は、位相が$-180°$の周波数において、利得が$0[dB]$からどのぐらい余裕があるのかを示しています。

通常のオペアンプでは、$-7～-10[dB]$程度で設計されており、位相余裕と同様に発振の余裕度として使われます。

スルー・レート/Slew Rate

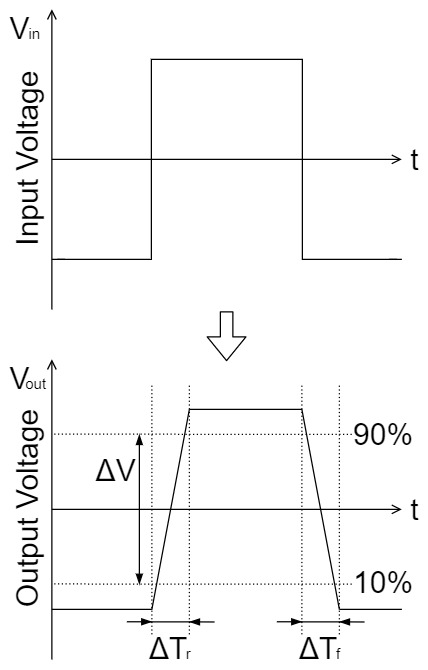
スルー・レート$SR$は、オペアンプの動作速度のことを言います。オペアンプの出力電圧が一定の単位時間あたりに変化できる割合を表します。
$$SR=\frac{ΔV}{ΔT}[V/s]$$
また、以下のように、立ち上がり時の時間$ΔT_r$、立ち下がり時の時間$ΔT_f$にわけてスルー・レート$SR$を表す場合もあります。
$$SR_r=\frac{ΔV}{ΔT_r}[V/s] \quad SR_f=\frac{ΔV}{ΔT_f}[V/s]$$
入力信号に対して忠実に出力信号を出力できればいいのですが、実物のオペアンプはスルー・レート$SR$と言う制限があります。

そのため、立ち上がりと立ち下がりが急激に変化する方形波をオペアンプに入力すると、出力電圧が追随できずに方形波が台形状に歪んでしまうのです。

また、正弦波についても周波数が高いと、同様に出力電圧が追随できずに三角波に波形が歪んでしまいます。

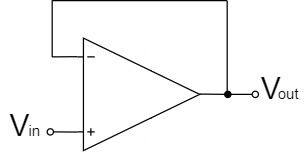
ここで、増幅率1倍のボルテージフォロアにおけるオペアンプが出力可能な周波数について求めると、以下のように算出することができます。

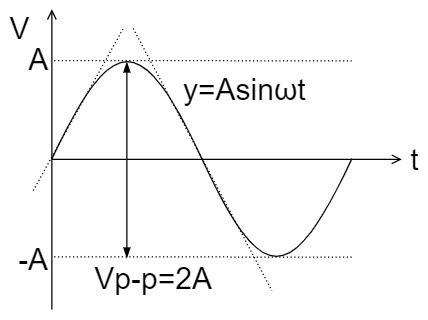
$$y=Asinωt$$
スルー・レート$SR$は、正弦波(sin波)の接線の傾きなので、上式$y$を微分します。
$$\frac{dy}{dt}=Aωcosωt, \quad ωt=0$$
よって、$ω=2πf, V_{p-p}=2A$なので、スルー・レート$SR$は、以下のようになります。
$$SR=\frac{dy}{dt}=Aωcosωt=Aωcos0=Aω=2πfA=πfV_{p-p}[V/s]$$
さらに、周波数$f$、電圧振幅$V_{p-p}$を求める式に変形することができます。
$$f=\frac{SR}{πV_{p-p}}[Hz], \quad V_{p-p}=\frac{SR}{πf}[V]$$
そのため、スルー・レート$SR$が大きく、電圧振幅が小さいほど、出力可能な周波数が高くなるということがわかります。

例として$SR=50[V/us]=50\times10^{6}[V/s]$、$V_{p-p}=1[V]$の時に出力可能な周波数を求めると以下のようになります。
$$f=\frac{SR}{πV_{p-p}}=\frac{50\times10^{6}}{π\times1}≒15.9[MHz]$$
なお、非反転増幅回路や反転増幅回路などでの増幅率$A_V$を加えると、以下の式になります。
$$f=\frac{SR}{πV_{p-p}A_V}[Hz], \quad V_{p-p}=\frac{SR}{πfA_V}[V]$$
この式からは増幅率が大きくなると、出力可能な周波数が低くなるということがわかります。

例として$SR=50[V/us]=50\times10^{6}[V/s]$、$V_{p-p}=1[V]$、$A_{V}=10[倍]$の時に出力可能な周波数を求めると以下のようになります。
$$f=\frac{SR}{πV_{p-p}A_V}=\frac{50\times10^{6}}{π\times1\times10}≒1.59[MHz]$$
増幅率$A_V$が1倍から10倍になると、出力可能な周波数が1/10になるのがわかります。

セトリング・タイム/Settling Time

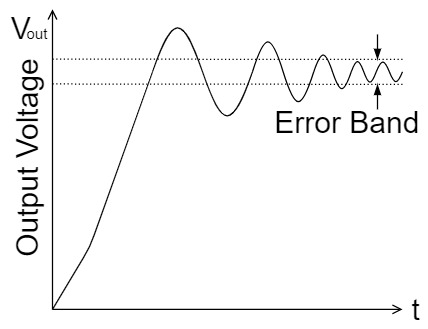
セトリング・タイム$t_s$は、オペアンプにステップ入力した時に、出力が一定の誤差範囲内まで収まるまでの時間のことを言います。

ステップ入力は電圧が急激に立ち上がるパルスを入力するので、出力電圧はスルーレートにより台形状になまったり、リンギングと呼ばれる電圧の振動が生じます。

セトリング・タイム$t_s$が短ければ、これらの現象が収束するまでの時間が短いということになります。

ノイズ/Noise

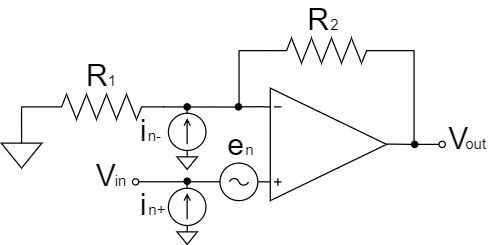
ここでは、オペアンプの電圧ノイズと電流ノイズに絞り、上図のような理想オペアンプの非反転増幅回路にノイズモデルが接続された状態で考えてきます。

以下のように、電圧ノイズ、電流ノイズは、低周波領域の「1/fノイズ」と高周波領域の「ホワイトノイズ」が存在します。
(細かく説明すると他にもノイズの種類はありますが、当記事では割愛します。)

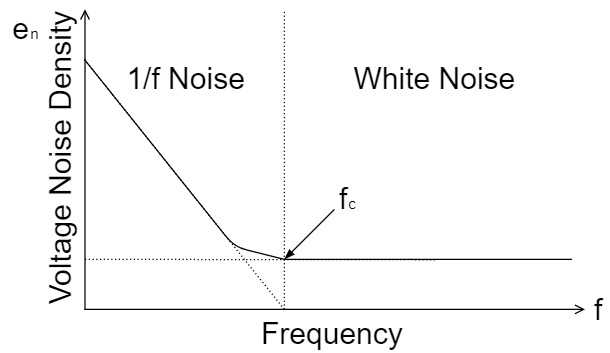
「1/fノイズ」はコーナー周波数$f_c$から反比例で$3[dB/oct]$増加しているのに対して、「ホワイトノイズ」は一定の状態になっています。

また、ノイズの単位として、電圧ノイズ密度$e_n$は$V/\sqrt{Hz}$、電流ノイズ密度$i_n$は$A/\sqrt{Hz}$が使われます。

入力電圧ノイズ/Input Voltage Noise

入力電圧ノイズ$e_{n}p-p$は、特に「1/fノイズ」を示す指標として、限定された周波数の帯域幅(例:0.1～10Hz)において「$V_{p-p}$」の単位で表す場合があります。

入力電圧ノイズ密度/Input Voltage Noise Density

入力電圧ノイズ密度$e_n$は、「$V/\sqrt{Hz}$」の単位で表し、特定の周波数の入力電圧ノイズ$V_n$を算出することができます。

例えば、$e_n=5[nV/\sqrt{Hz}]$、$f=100[kHz]$の場合、以下のように計算できます。
$$V_n=e_n\times\sqrt{f}=5\times\sqrt{100\times1000}=1581[nV]$$
また、$e_n=5[nV/\sqrt{Hz}]$、$f=1000[kHz]$の場合、以下のように計算できます。
$$V_n=e_n\times\sqrt{f}=5\times\sqrt{1000\times1000}=5000[nV]$$
仮に入力電圧ノイズ$V_n$が高いとすると、このままオペアンプで増幅されてしまうので、微弱な入力信号の場合、ノイズに埋もれてしまうことになります。

入力電流ノイズ密度/Input Current Noise Density

入力電流ノイズ密度$i_n$は、「$A/\sqrt{Hz}$」の単位で表します。

電流値のままだとわかりづらいので、この入力電流ノイズ密度$i_n$を入力電圧ノイズ密度に変換して、先程説明した入力電圧ノイズ密度$e_n$と合計します。

計算を簡単にするため、$i_n=i_{n+}=i_{n-}$と仮定すると、入力電圧ノイズ密度$e_n$と入力電流ノイズ密度$i_n$を合計した入力電圧ノイズ$V_n$は以下のようになります。
$$V_n=\sqrt{e_n^2+\left(\frac{R_1R_2}{R_1+R_2}\right)^2i_n^2}[V]$$
入力電流ノイズ密度$i_n$はオペアンプの外付け抵抗が影響しており、抵抗値が高いとノイズが増加することがわかります。

ただし、オペアンプにもよりますが、入力電圧ノイズ密度$e_n$が「$nV/\sqrt{Hz}$」オーダー($10^{-9}$オーダー)なのに対して、入力電流ノイズ密度$i_n$は「$fA/\sqrt{Hz}$」オーダー($10^{-15}$オーダー)と非常に小さいので、よほど抵抗値が高くない限り無視できるレベルです。