オペアンプの比較回路(コンパレータ)
当記事では、「オペアンプ(OPアンプ/OP-Amp)の比較回路(コンパレータ)」について詳しく解説していきます。
比較回路は負帰還をかけずに開ループで使用するのが特徴で、二つの入力信号を比較して$+V_{CC}(HIGH)$または$-V_{CC}(LOW)$で出力します。
実用回路としては、しきい値付近のばたつきを抑えるため、ヒステリシス特性を持った比較回路が使われることが多いです。
また、オペアンプを使って比較回路を作る以外に、専用のコンパレータICも存在します。
オペアンプの比較回路(コンパレータ)の特徴
「比較回路(コンパレータ)」と「ヒステリシス付き比較回路(ヒステリシス付きコンパレータ)」にわけて、オペアンプの比較回路の特徴について解説していきます。
比較回路(コンパレータ)
$$V_{out}=+V_{CC} \quad (V_{in+}>V_{in-})$$
$$V_{out}=-V_{CC} \quad (V_{in+} \lt V_{in-})$$
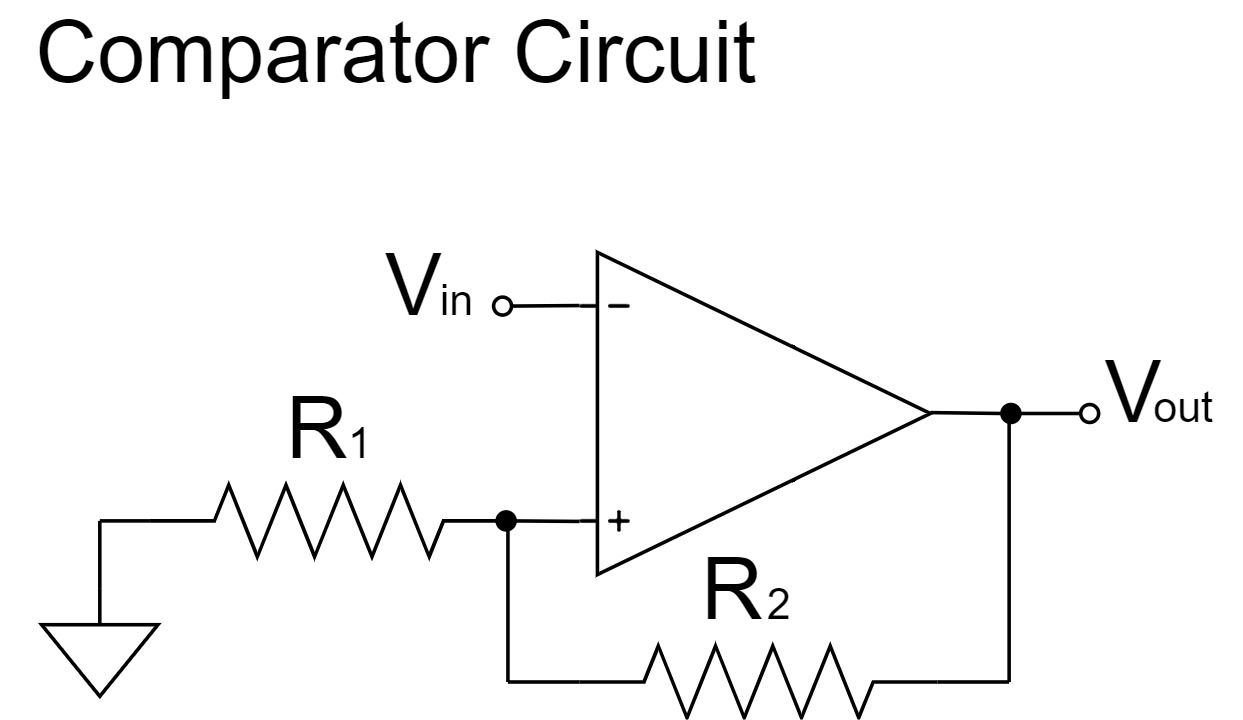
比較回路(コンパレータ)は、負帰還をかけずに、開ループで動作させます。
非反転入力$V_{in+}$と反転入力$V_{in-}$の大小関係に従って出力が決まるので、上式の通り、$V_{in+}>V_{in-}$の時は+側の電源電圧$+V_{CC}$で飽和し、$V_{in+} \lt V_{in-}$の時は-側の電源電圧$-V_{CC}$で飽和します。
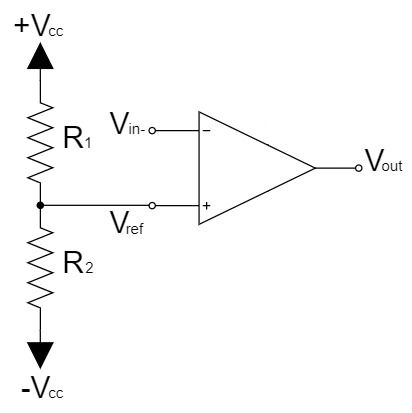
ただ、実際の使い方としては、今まで説明したような別個の2つの電圧を比較するより、一方の入力に基準電圧を与え、もう一方の入力に加えられる入力電圧を基準電圧と比較する使い方が多いです。
以下のように、大きくわけて、入力電圧を反転入力または非反転入力にする回路があります。出力電圧が反転するしないの違いだけで特性的な違いはありません。
$$V_{out}=-V_{CC} \quad (V_{in-}>V_{ref})$$
$$V_{out}=+V_{CC} \quad (V_{in-} \lt V_{ref})$$
まず、入力電圧を反転入力にした場合、上式の通り、$V_{in-}>V_{ref}$の時は-側の電源電圧$-V_{CC}$で飽和し、$V_{in-} \lt V_{ref}$の時は+側の電源電圧$+V_{CC}$で飽和します。
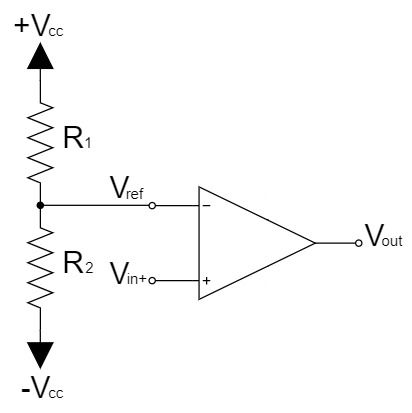
$$V_{out}=+V_{CC} \quad (V_{in+}>V_{ref})$$
$$V_{out}=-V_{CC} \quad (V_{in+} \lt V_{ref})$$
次に、入力電圧を非反転入力にした場合、上式の通り、$V_{in+}>V_{ref}$の時は+側の電源電圧$+V_{CC}$で飽和し、$V_{in+} \lt V_{ref}$の時は-側の電源電圧$-V_{CC}$で飽和します。
ヒステリシス付き比較回路(ヒステリシス付きコンパレータ)
開ループで動作する比較回路(コンパレータ)に正帰還をかけることで、基準電圧にヒステリシス特性を持たせることができます。
以下のように、大きくわけて、入力電圧を反転入力または非反転入力にする回路があります。$V_{refH}$と$V_{refL}$の計算方法がそれぞれの回路で異なるので注意して下さい。
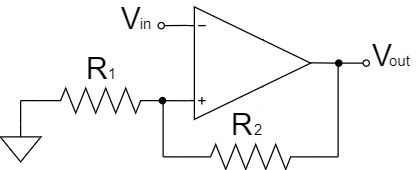
$$V_{out}=-V_{CC} \quad (V_{in-}>V_{refH}) \quad V_{refH}=\frac{R_1}{R_1+R_2}V_{CC}$$
$$V_{out}=+V_{CC} \quad (V_{in-} \lt V_{refL}) \quad V_{refL}=-\frac{R_1}{R_1+R_2}V_{CC}$$
まず、入力電圧を反転入力にした場合、上式の通り、$V_{in-}>V_{refH}$の時は-側の電源電圧$-V_{CC}$で飽和し、$V_{in-} \lt V_{refL}$の時は+側の電源電圧$+V_{CC}$で飽和します。
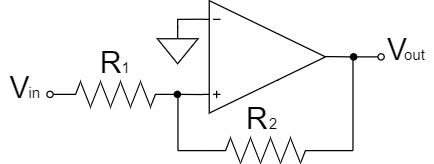
$$V_{out}=+V_{CC} \quad (V_{in+}>V_{refH}) \quad V_{refH}=\frac{R_1}{R_2}V_{CC}$$
$$V_{out}=-V_{CC} \quad (V_{in+} \lt V_{refL}) \quad V_{refL}=-\frac{R_1}{R_2}V_{CC}$$
次に、入力電圧を非反転入力にした場合、上式の通り、$V_{in+}>V_{refH}$の時は+側の電源電圧$+V_{CC}$で飽和し、$V_{in+} \lt V_{refL}$の時は-側の電源電圧$-V_{CC}$で飽和します。
ヒステリシス特性なし
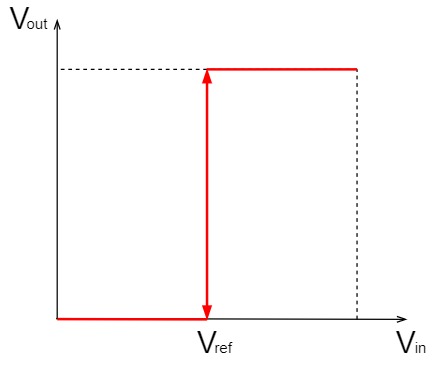
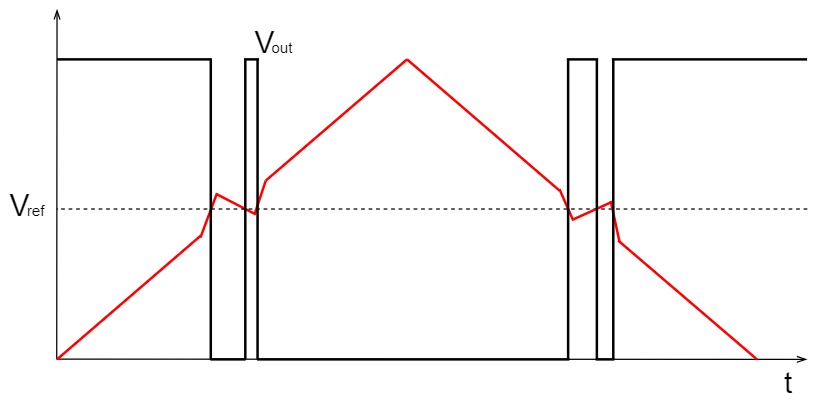
入力信号にノイズが含まれている場合、ばたつきを防ぐため、比較回路にヒステリシス特性は必須となります。
上図のように、しきい値付近でノイズが発生すると、ヒステリシス特性がないと出力がばたついてしまいます。
ヒステリシス特性あり
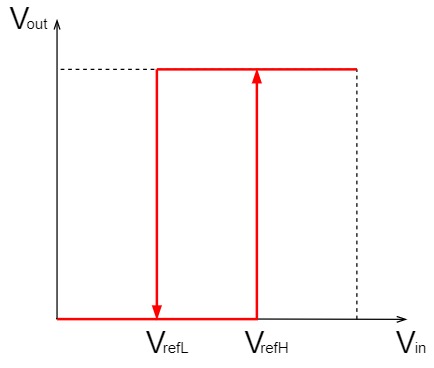
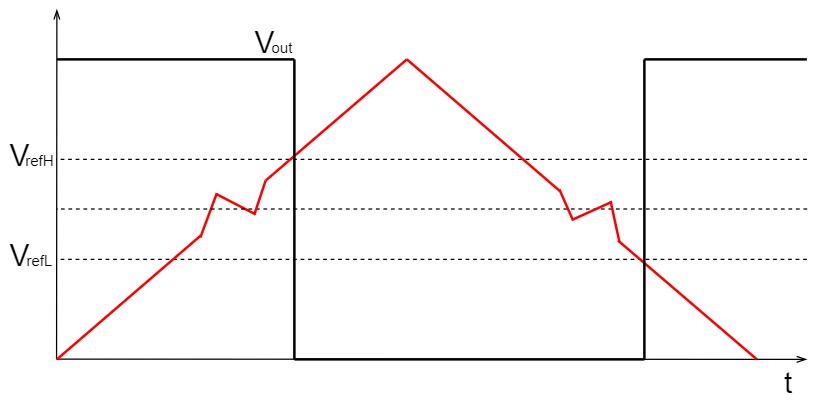
一方、ヒステリシス特性がついていると、$V_{refH}$と$V_{refL}$の間であれば出力がばたつかなくなります。
オペアンプのヒステリシス付き比較回路(ヒステリシス付きコンパレータ)の計算
「反転ヒステリシス付き比較回路(反転ヒステリシス付きコンパレータ)」と「非反転ヒステリシス付き比較回路(反転ヒステリシス付きコンパレータ)」にわけて、回路各部の電圧の関係式から算出する精密計算をします。
反転ヒステリシス付き比較回路(反転ヒステリシス付きコンパレータ)の計算
反転ヒステリシス付き比較回路

$$V_{out}=-V_{CC} \quad (V_{in-}>V_{refH})$$
$$V_{out}=+V_{CC} \quad (V_{in-} \lt V_{refL})$$
反転ヒステリシス付き比較回路で基準電圧となる$V_{refH}$と$V_{refL}$を求めていきます。
オペアンプの$+$端子は入力インピーダンスが高く、電流が流れ込まないことから、以下のような回路で表すことができます。
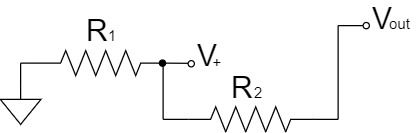
これで、分圧回路として簡単に$V_+$を求めることができます。
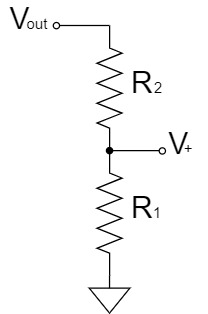
$$V_+=\frac{R_1}{R_1+R_2}V_{out}$$
$V_{ref}=V_+$なので、$V_ref$は以下の通りになります。
$$V_{ref}=\frac{R_1}{R_1+R_2}V_{out}$$
さらに、$V_{refH}$と$V_{refL}$を求めるには、「$V_{in}$が$-V_{CC}$から$+V_{CC}$に上昇する時」と「$V_{in}$が$+V_{CC}$から$-V_{CC}$に下降する時」の2つの状態を考えてそれぞれ導いていきます。
- $V_{refH}$: $V_{in}=-V_{CC} ⇒ V_{in}=+V_{CC}$($V_{in}$が$-V_{CC}$から$+V_{CC}$に上昇する時)
- $V_{refL}$: $V_{in}=+V_{CC} ⇒ V_{in}=-V_{CC}$($V_{in}$が$+V_{CC}$から$-V_{CC}$に下降する時)
まずは、$V_{in}$が$-V_{CC}$から$+V_{CC}$に上昇する時を考えてみます。
$V_{in}(V_{in-})$が$-V_{CC}$であれば、$V_{in-}$はオペアンプで扱える電圧範囲で最も低くなるので、$V_{in-}$は必ず$V_{in+}$よりも小さくなります。
$V_{in+}$が$V_{in-}$より大きいことから、$V_{out}$は$+V_{CC}$になります。
$$V_{in}=V_{in-}=-V_{CC}⇒V_{in-}<V_{in+}$$
$$V_{out}=+V_{CC} \quad (V_{in-}<V_{in+})$$
そのため、$V_{refH}$は、以下のようになります。
$$V_{refH}=\frac{R_1}{R_1+R_2}V_{out}=\frac{R_1}{R_1+R_2}(+V_{CC})=\frac{R_1}{R_1+R_2}V_{CC}$$
そして、$V_{in}$が$-V_{CC}$から$+V_{CC}$に上昇する過程で$V_{refH}$に到達すると、$V_{out}$は$-V_{CC}$に切り替わり、しきい値も$V_{refH}$から$V_{refL}$に切り替わります。
次に$V_{in}$が$+V_{CC}$から$-V_{CC}$に下降する時を考えてみます。
$V_{in}(V_{in-})$が$+V_{CC}$であれば、$V_{in-}$はオペアンプで扱える電圧範囲で最も高くなるので、$V_{in-}$は必ず$V_{in+}$よりも大きくなります。
$V_{in-}$が$V_{in+}$より大きいことから、$V_{out}$は$-V_{CC}$になります。
$$V_{in}=V_{in-}=+V_{CC}⇒V_{in-}>V_{in+}$$
$$V_{out}=-V_{CC} \quad (V_{in-}>V_{in+})$$
そのため、$V_{refL}$は、以下のようになります。
$$V_{refL}=\frac{R_1}{R_1+R_2}V_{out}=\frac{R_1}{R_1+R_2}(-V_{CC})=-\frac{R_1}{R_1+R_2}V_{CC}$$
そして、$V_{in}$が$+V_{CC}$から$-V_{CC}$に下降する過程で$V_{refL}$に到達すると、$V_{out}$は$+V_{CC}$に切り替わり、しきい値も$V_{refL}$から$V_{refH}$に切り替わります。
非反転ヒステリシス付き比較回路(反転ヒステリシス付きコンパレータ)の計算
非反転ヒステリシス付き比較回路

$$V_{out}=+V_{CC} \quad (V_{in+}>V_{refH})$$
$$V_{out}=-V_{CC} \quad (V_{in+} \lt V_{refL})$$
非反転ヒステリシス付き比較回路で基準電圧となる$V_{refH}$と$V_{refL}$を求めていきます。
オペアンプの$+$端子は入力インピーダンスが高く、電流が流れ込まないことから、以下のような回路で表すことができます。
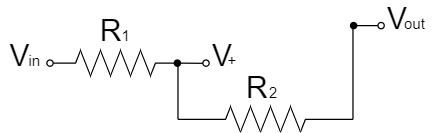
重ね合わせの理(重ね合わせの原理、重ねの理、重畳の理)により、上記の回路を2つに分割して考えると、分圧回路として簡単に$V_+$を求めることができます。
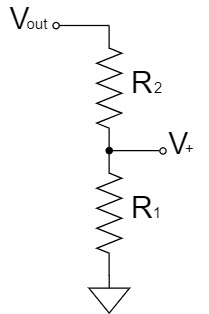
$$V_{1+}=\frac{R_1}{R_1+R_2}V_{out}$$
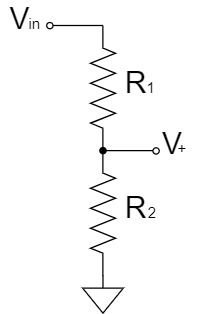
$$V_{2+}=\frac{R_2}{R_1+R_2}V_{in}$$
よって、$V_+$は以下のようになります。
$$V_{+}=V_{1+}+V_{2+}$$
$$V_+=\frac{R_1}{R_1+R_2}V_{out}+\frac{R_2}{R_1+R_2}V_{in}$$
$V_-$はGNDに固定されて$0[V]$となっているので、$V_+=0$の時の$V_{in}$の電圧値がしきい値になります。
$$0=\frac{R_1}{R_1+R_2}V_{out}+\frac{R_2}{R_1+R_2}V_{in}$$
$$\frac{R_2}{R_1+R_2}V_{in}=-\frac{R_1}{R_1+R_2}V_{out}$$
$$R_2V_{in}=-R_1V_{out}$$
$$V_{in}=-\frac{R_1}{R_2}V_{out}$$
$V_{ref}=V_{in}$なので、$V_{ref}$は以下の通りになります。
$$V_{ref}=-\frac{R_1}{R_2}V_{out}$$
さらに、$V_{refH}$と$V_{refL}$を求めるには、「$V_{in}$が$-V_{CC}$から$+V_{CC}$に上昇する時」と「$V_{in}$が$+V_{CC}$から$-V_{CC}$に下降する時」の2つの状態を考えてそれぞれ導いていきます。
- $V_{refH}$: $V_{in}=-V_{CC} ⇒ V_{in}=+V_{CC}$($V_{in}$が$-V_{CC}$から$+V_{CC}$に上昇する時)
- $V_{refL}$: $V_{in}=+V_{CC} ⇒ V_{in}=-V_{CC}$($V_{in}$が$+V_{CC}$から$-V_{CC}$に下降する時)
まずは、$V_{in}$が$-V_{CC}$から$+V_{CC}$に上昇する時を考えてみます。
$V_{in}$が$-V_{CC}$であれば、$V_{out}$も$-V_{CC}$になります。
そのため、$V_{refH}$は、以下のようになります。
$$V_{refH}=-\frac{R_1}{R_2}V_{out}=-\frac{R_1}{R_2}(-V_{CC})=\frac{R_1}{R_2}V_{CC}$$
そして、$V_{in}$が$-V_{CC}$から$+V_{CC}$に上昇する過程で$V_{refH}$に到達すると、$V_{out}$は$+V_{CC}$に切り替わり、しきい値も$V_{refH}$から$V_{refL}$に切り替わります。
次に$V_{in}$が$+V_{CC}$から$-V_{CC}$に下降する時を考えてみます。
$V_{in}$が$+V_{CC}$であれば、$V_{out}$も$+V_{CC}$になります。
そのため、$V_{refL}$は、以下のようになります。
$$V_{refL}=-\frac{R_1}{R_2}V_{out}=-\frac{R_1}{R_2}(+V_{CC})=-\frac{R_1}{R_2}V_{CC}$$
そして、$V_{in}$が$+V_{CC}$から$-V_{CC}$に下降する過程で$V_{refL}$に到達すると、$V_{out}$は$-V_{CC}$に切り替わり、しきい値も$V_{refL}$から$V_{refH}$に切り替わります。
その他のオペアンプの回路例
当記事では、「オペアンプの比較回路(コンパレータ)」について詳しく解説してきましたが、その他にもオペアンプには様々な回路が存在します。
以下の記事で、比較的よく使われるオペアンプの回路について紹介しているので、ぜひご覧ください。