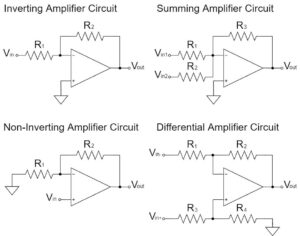
オペアンプの電圧フォロワ(ボルテージフォロワ)
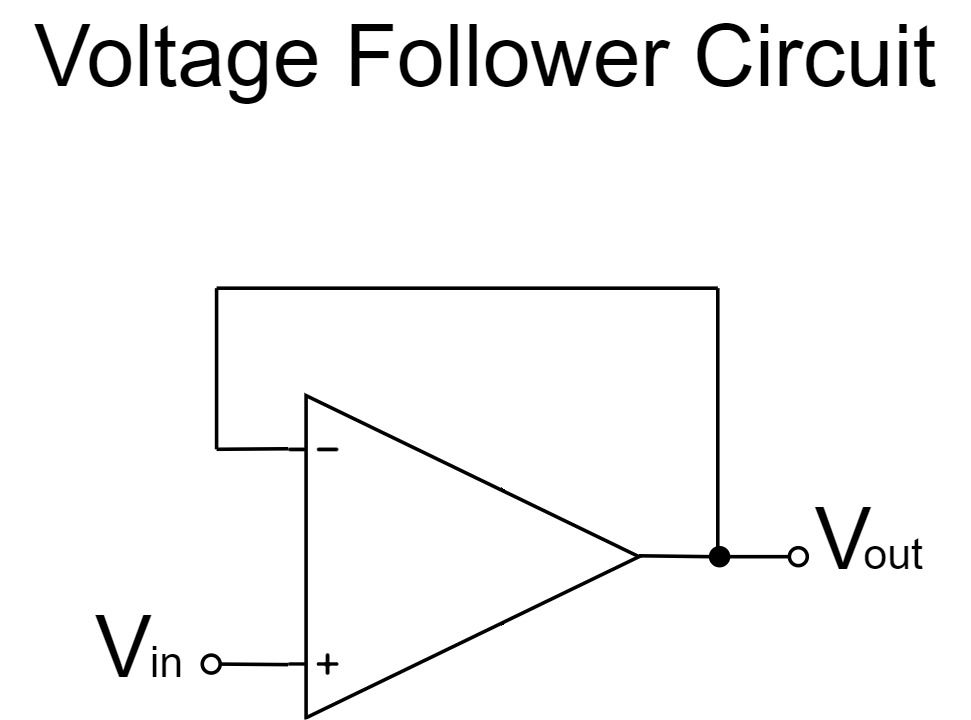
当記事では、「オペアンプ(OPアンプ/OP-Amp)の電圧フォロワ(ボルテージフォロワ)」について詳しく解説していきます。
電圧フォロワは、オペアンプの出力端子が反転端子に接続(負帰還)されただけの簡単な回路で、インピーダンス変換や回路の分離に使われることが多いです。
電圧フォロワの特徴
電圧フォロワ
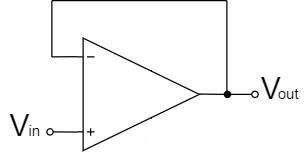
$$V_{out}=V_{in}$$
電圧フォロワは、上式の通り、1倍の増幅率で、$V_{in}$の信号がそのまま$V_{out}$に出力されます。
例えば、$V_{in}=1V$であれば、$V_{out}=1V$になります。
$$V_{out}=1[V]$$
また、電圧フォロワは、増幅率1倍の非反転増幅回路なので、電圧フォロワの特徴と非反転増幅回路の特徴はほぼ共通しています。
- 出力信号が入力信号に対して反転しない
- 増幅率は1倍
- 電気的に動作が不安定
- 入力インピーダンスが非常に高い
- 出力インピーダンスがほぼ0
出力信号が入力信号に対して反転しない
電圧フォロワは、出力信号が入力信号に対して反転しないため、入力信号と出力信号の位相が同じになります。
例えば、入力電圧が+であれば出力電圧は+、入力電圧が-であれば出力電圧は-になるということです。
増幅率は1倍
電圧フォロワは、増幅率1倍になります。
増幅率1倍の回路に意味があるのか疑問を感じる方もいるかもしれませんが、「インピーダンス変換」や「回路の分離」によく使われます。
インピーダンス変換
センサなど信号源側(Signal Source)の出力インピーダンスが高く、負荷側(Load)の入力インピーダンスが低い場合、電圧降下が生じてしまい、正確な電圧が負荷側に伝わらなくなってしまいます。
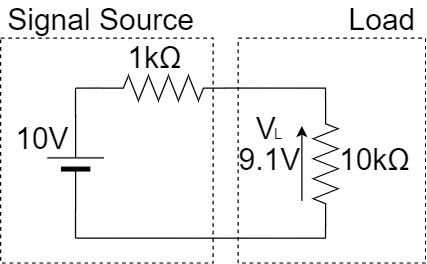
上記のように、信号源が電圧$10[V]$、出力インピーダンス$1[kΩ]$の場合、$10[kΩ]$の負荷を接続すると負荷電圧$V_L$は以下のようになります。
$$V_L=\frac{10kΩ}{1kΩ+10kΩ} \times 10V \fallingdotseq 9.1[V]$$
このように、負荷電圧$V_L$は約$9.1[V]$となってしまい、本来は$10[V]$の電圧が印加されるはずが10%近くの誤差が生じてしまうのです。
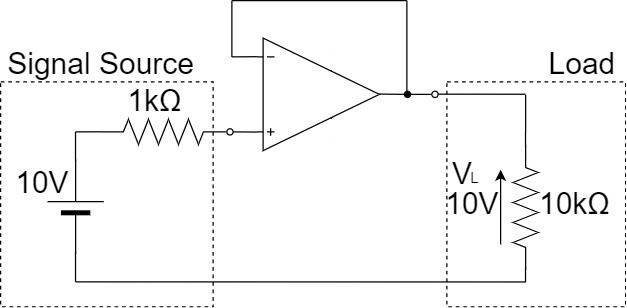
そこで、上記のように、電圧フォロワを信号源と負荷の間にバッファとして使って、インピーダンス変換を行うことで、正確な電圧を伝えることが可能です。
電圧フォロワの入力インピーダンスは高く、出力インピーダンスは低いので、信号源の電圧$10[V]$を電圧降下を生じさせずそのまま負荷側に伝えることができます。
回路の分離
分圧回路に負荷抵抗を接続すると抵抗値が変化してしまうため、正確な電圧が負荷側に伝わらなくなってしまいます。
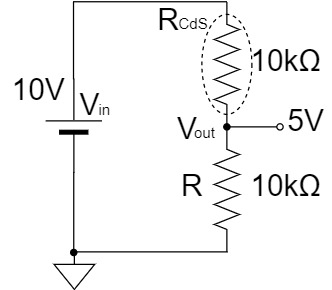
上記のように、CdS(光センサ) GL5528は入射する光によって抵抗値が変化して、暗い時に約$1[MΩ]$ある抵抗値が、明るい時は約$10[kΩ]$まで下がります。
(CdS GL5528の明抵抗は、10Lux時に10~20[kΩ]と幅がありますが、当記事ではわかりやすさ優先のため10[kΩ]として解説します。)

そのため、以下のように明るい時であれば、入力電圧$V_{in}$が$10[V]$だと、出力電圧$V_{out}$は$5[V]$となります。
$$V_{out}=\frac{R}{R_{CdS}+R} \times V_{in} = \frac{10kΩ}{10kΩ+10kΩ} \times 10V = 5[V]$$
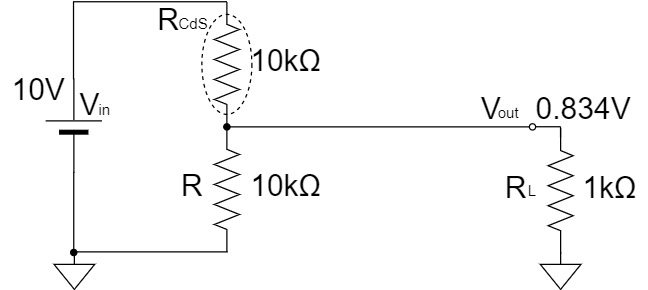
しかし、負荷抵抗$R_{L}$を接続すると、$R$と$R_{L}$による合成抵抗により、出力電圧$V_{out}$は約$0.834[V]$となってしまいます。
$$R//R_{L}=\frac{R \times R_{L}}{R + R_{L}} = \frac{10k \times 1k}{10k + 1k} \fallingdotseq 0.91[kΩ]$$
$$V_{out}=\frac{R//R_{L}}{R_{CdS}+R//R_{L}} \times V_{in} = \frac{0.91k}{10k+0.91k} \times 10 \fallingdotseq 0.834[V]$$
つまり、明るい状態なのにもかかわらず、暗い状態を示しているのです。
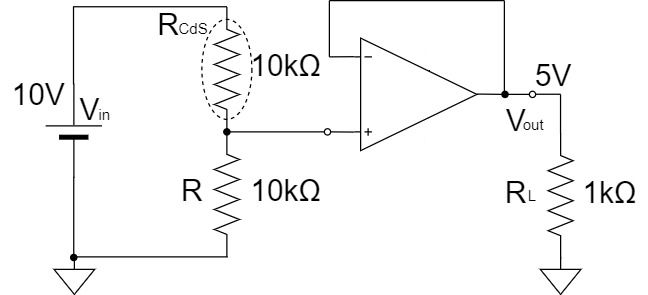
そこで、上記のように、電圧フォロワを分圧回路と負荷抵抗の間に使って、回路の分離を行うことで、正確な電圧を伝えることが可能です。
電圧フォロワの入力インピーダンスは高く、出力インピーダンスは低いので、入力電圧$10[V]$を電圧降下を生じさせずそのまま負荷側に伝えることができます。
電気的に動作が不安定
電圧フォロワは、反転増幅回路と比較すると電気的に動作が不安定です。
オペアンプでは、$+$と$-$の端子がオペアンプ内部で仮想的に接続(仮想短絡/イマジナリショート/バーチャルショート)されています。
電圧フォロワの場合、$+$端子に入力される電圧によって動作点が振られてしまい、仮想短絡を通じて接続されている$-$の端子も同様に影響を受けてしまいます。
そのため、動作点が入力電圧によって振られることから、入力信号が直流や低周波であれば問題ありませんが、高周波となると動作が不安定になる恐れがあるのです。
入力インピーダンスが非常に高い
電圧フォロワは、入力電圧が直接、$+$端子に入力されるため、入力インピーダンスが非常に高くなります。
(一般的に、オペアンプの$+$と$-$の入力端子は、どちらも入力インピーダンスが非常に高いです。)
そのため、電圧フォロワの入力に接続する回路のインピーダンスがある程度高くても、ほとんど影響を受けることなく電圧降下が生じてしまうことはありません。精度の高い測定などに向いていると言えるでしょう。
出力インピーダンスがほぼ0
電圧フォロワの出力インピーダンスは、負帰還の働きによって$V_{out}=V_{in}$の関係式を満たす電圧に保たれているので、ほぼ0になります。
そのため、オペアンプの出力端子に接続する回路の入力インピーダンスのほとんど影響を受けず、電圧降下を起こさずに必要な信号レベルを取り出すことができます。
電圧フォロワの計算
電圧フォロワの関係式を求めるために、「負帰還と仮想短絡からの計算」と「非反転増幅回路からの計算」をします。
負帰還と仮想短絡からの計算
電圧フォロワ

電圧フォロワの場合、負帰還をかけるため$V_{out}$と$V_-$が直接、接続されてるので以下のようになります。
$$V_{out}=V_-$$
また、電圧フォロワは、$V_+$と$V_{in}$が同じなります。
$$V_+=V_{in}$$
さらに、オペアンプでは、$+$と$-$の端子がオペアンプ内部で仮想的に接続(仮想短絡/イマジナリショート/バーチャルショート)されています。
$$V_+=V_-$$
以上により、電圧フォロワの$V_{out}$は以下のようになります。
$$V_{out}=V_{in}$$
非反転増幅回路からの計算
非反転増幅回路
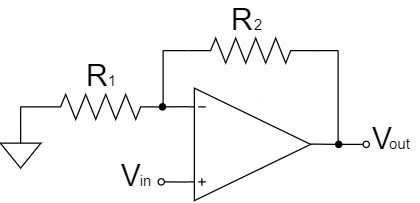
電圧フォロワは、非反転増幅回路の抵抗$R_1$を開放(∞Ω)、$R_2$を短絡(0Ω)にした回路と見なすことができます。
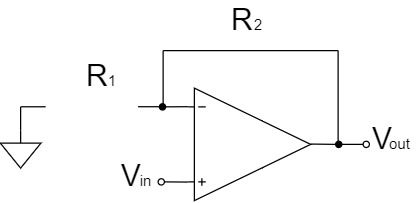
そのため、以下のように非反転増幅回路の関係式から電圧フォロワの関係式を算出することができます。
$$V_{out}=\left(1+\frac{R_2}{R_1}\right)V_{in}=\left(1+\frac{0}{∞}\right)V_{in}$$
$$V_{out}=V_{in}$$
なお、非反転増幅回路の関係式の算出は以下の記事をご覧下さい。
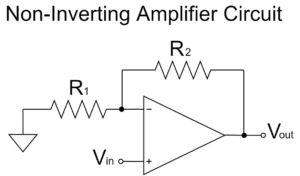
その他のオペアンプの回路例
当記事では、「電圧フォロワ(ボルテージフォロワ)」について詳しく解説してきましたが、その他にもオペアンプには様々な回路が存在します。
以下の記事で、比較的よく使われるオペアンプの回路について紹介しているので、ぜひご覧ください。