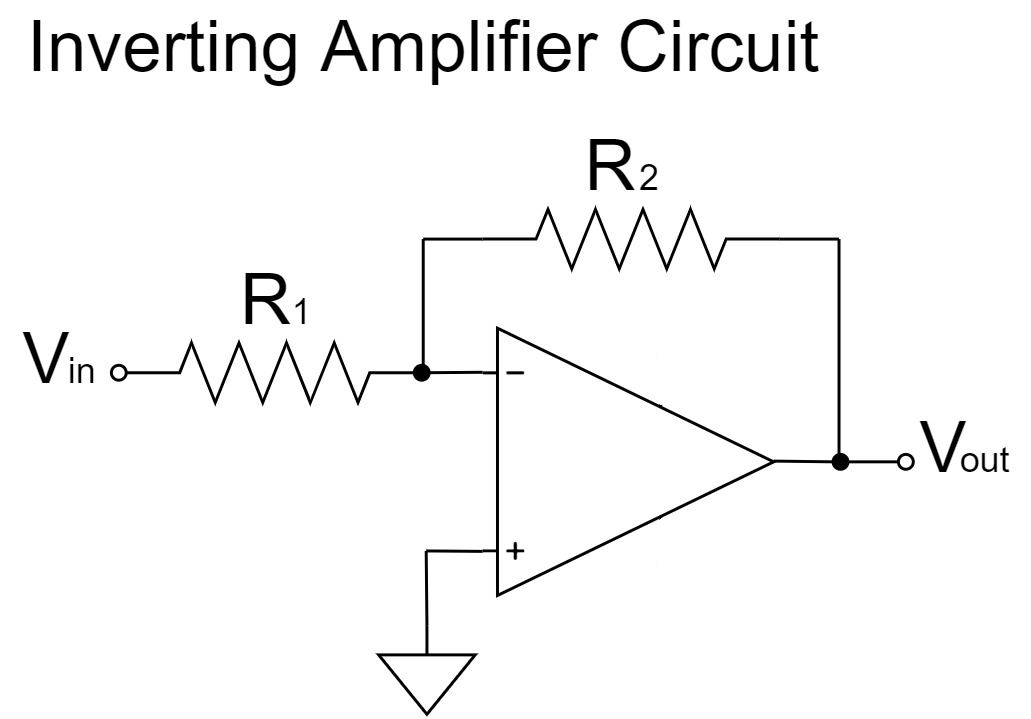
オペアンプの反転増幅回路
当記事では、「オペアンプ(OPアンプ/OP-Amp)の反転増幅回路」について詳しく解説していきます。
反転増幅回路は、オペアンプの中で最も基本的な回路で、その他の応用回路に使われることが多いです。
オペアンプの反転増幅回路の特徴
反転増幅回路
$$V_{out}=-\frac{R_2}{R_1}V_{in}$$
反転増幅回路は、上式の通り、$\frac{R_2}{R_1}$の増幅率で、$V_{in}$の信号が増幅され、$V_{out}$に出力されます。また、「$-$」の極性が表す通り、$V_{out}$の信号は反転されます。
例えば、$R_1=1kΩ, R_2=10kΩ, V_{in}=1V$であれば、$V_{out}=-10V$になります。
$$V_{out}=-\frac{10k}{1k} \times 1=-10[V]$$
- 出力信号が入力信号に対して反転する
- 増幅率の設定範囲が広い(バッファ、減衰器も可能)
- 電気的に動作が安定
- 入力インピーダンスが入力抵抗
- 出力インピーダンスがほぼ0
出力信号が入力信号に対して反転する
オペアンプの反転増幅回路は、出力信号が入力信号に対して反転するため、入力信号と出力信号の位相が180°異なります。
例えば、入力電圧が+であれば出力電圧は-、入力電圧が-であれば出力電圧は+になるということです。
信号を反転したくない場合は、反転増幅回路を2段直列に接続すれば、「反転+反転⇒正転」となります。
増幅率の設定範囲が広い(バッファ、減衰器も可能)
オペアンプの反転増幅回路の比率は$\frac{R_2}{R_1}$となっているので、増幅率の設定範囲が広いです。
そのため、$R_2 \gt R_1$であれば増幅器、$R_2=R_1$なら増幅率1倍のバッファ、$R_2 \lt R_1$なら減衰器と様々な反転増幅回路を作ることができます。
(増幅率1倍以下であっても反転増幅回路と呼びます。)
電気的に動作が安定
オペアンプの反転増幅回路は、電気的に動作が安定しています。
オペアンプでは、$+$と$-$の端子がオペアンプ内部で仮想的に接続(仮想短絡/イマジナリショート/バーチャルショート)されています。
反転増幅回路の場合、$+$端子がGNDに接続されているので、仮想短絡を通じて$-$端子もGNDに接続されていると考えることができるのです。
そのため、動作点がGNDの電位(0V)に固定されており、反転増幅回路は回路特性が良好で、その他の応用回路にも使われやすいメリットがあります。
入力インピーダンスが入力抵抗
オペアンプの反転増幅回路は、入力インピーダンスが入力抵抗になるので、$R_1$が入力インピーダンスとなります。
「電気的に動作が安定」で説明した通り、$+$と$-$の端子がオペアンプ内部で仮想的に接続(仮想短絡/イマジナリショート/バーチャルショート)されていると考えることができます。
反転増幅回路の場合、$+$端子がGNDに接続されているので、仮想短絡を通じて$-$端子もGNDに接続されていると考えることができるのです。
よって、反転増幅回路の入力側から見れば、$R_1$はGNDに接続されている状態になるので、$R_1$が入力インピーダンスとなるのです。
そのため、反転増幅回路の入力に接続する回路のインピーダンスが高く、反転増幅回路の入力インピーダンスが低すぎると、電圧降下が生じてしまい正しい電圧が伝われなくなってしまいます。
出力インピーダンスがほぼ0
オペアンプの反転増幅回路の出力インピーダンスは、負帰還の働きによって$V_{out}=-\frac{R_2}{R_1}V_{in}$の関係式を満たす電圧に保たれているので、ほぼ0になります。
そのため、オペアンプの出力端子に接続する回路の入力インピーダンスのほとんど影響を受けず、電圧降下を起こさずに必要な信号レベルを取り出すことができます。
オペアンプの反転増幅回路の計算
オペアンプの反転増幅回路の関係式を求めるために、回路各部の電圧の関係式から算出する精密計算と理想オペアンプをヌラーモデルに置き換えた簡易計算をします。
精密計算1
オペアンプの回路図記号
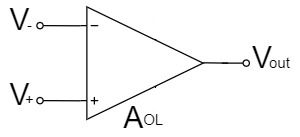
オペアンプは、$V_+$と$V_-$の2つの入力電圧の電位差をオープンループゲイン$A_{OL}$(開放利得$A_{OL}$)で増幅します。
$$V_{out}=A_{OL}(V_+-V_-)$$
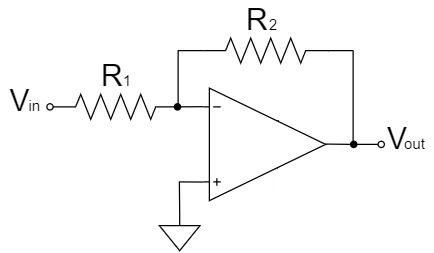
反転増幅回路

オペアンプの反転増幅回路の場合、$+$端子がGNDに接続されているので、$V_+$は0[V]になります。
$$V_+=0$$
以上により、反転増幅回路の$V_{out}$は以下のようになります。
$$V_{out}=A_{OL}(0-V_-)=-A_{OL}V_-\cdots(1)$$
また、反転増幅回路の$-$端子は入力インピーダンスが高く、電流が流れ込まないことから、以下のような回路で表すことができます。
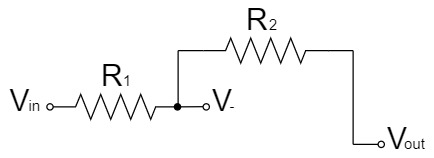
重ね合わせの理(重ね合わせの原理、重ねの理、重畳の理)により、上記の回路を2つに分割して考えると、分圧回路として簡単に$V_-$を求めることができます。
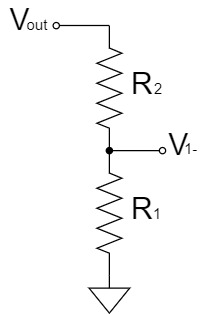
$$V_{1-}=\frac{R_1}{R_1+R_2}V_{out}$$
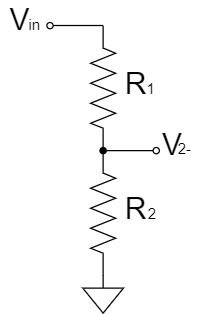
$$V_{2-}=\frac{R_2}{R_1+R_2}V_{in}$$
よって、$V_-$は以下のようになります。
$$V_{-}=V_{1-}+V_{2-}$$
$$V_-=\frac{R_1}{R_1+R_2}V_{out}+\frac{R_2}{R_1+R_2}V_{in}\cdots(2)$$
(1)式に(2)式を代入することで、$V_{out}$を計算していきます。
$$V_{out}=-A_{OL}\left(\frac{R_1}{R_1+R_2}V_{out}+\frac{R_2}{R_1+R_2}V_{in}\right)$$
$$V_{out}=-\frac{R_1}{R_1+R_2}A_{OL}V_{out}-\frac{R_2}{R_1+R_2}A_{OL}V_{in}$$
$$V_{out}+\frac{R_1}{R_1+R_2}A_{OL}V_{out}=-\frac{R_2}{R_1+R_2}A_{OL}V_{in}$$
$$\frac{R_1+R_2}{R_1+R_2}V_{out}+\frac{A_{OL}R_1}{R_1+R_2}V_{out}=-\frac{R_2}{R_1+R_2}A_{OL}V_{in}$$
$$\frac{R_1+R_2+A_{OL}R_1}{R_1+R_2}V_{out}=-\frac{R_2}{R_1+R_2}A_{OL}V_{in}$$
$$V_{out}=-\frac{R_2}{R_1+R_2+A_{OL}R_1}A_{OL}V_{in}$$
$$V_{out}=-\frac{A_{OL}R_2}{R_1+R_2+A_{OL}R_1}V_{in}$$
$$V_{out}=-\frac{R_2}{R_1}\frac{A_{OL}}{1+\frac{R_2}{R_1}+A_{OL}}V_{in}$$
$$V_{out}=-\frac{R_2}{R_1}\frac{1}{\frac{1}{A_{OL}}+\frac{1}{A_{OL}}\frac{R_2}{R_1}+1}V_{in}$$
$$V_{out}=-\frac{R_2}{R_1}\frac{1}{\frac{1}{A_{OL}}(1+\frac{R_2}{R_1})+1}V_{in}$$
ここで、$A_{OL}$は極めて大きい値(∞)であることを考えると、$\frac{1}{A_{OL}}⇒0$になります。よって、最終的な$V_{out}$は以下のようになります。
$$V_{out}=-\frac{R_2}{R_1}V_{in}$$
精密計算2
反転増幅回路

オペアンプの反転増幅回路の場合、$+$端子がGNDに接続されているので、$V_+$は0[V]になります。
$$V_+=0$$
さらに、$+$と$-$の端子は、仮想短絡(イマジナリショート/バーチャルショート)を通じて接続されていると考えることができます。
$$V_-=V_+=0\cdots(1)$$
また、反転増幅回路の$-$端子は入力インピーダンスが高く、電流が流れ込まないことから、以下のような回路で表すことができます。

重ね合わせの理(重ね合わせの原理、重ねの理、重畳の理)により、上記の回路を2つに分割して考えると、分圧回路として簡単に$V_-$を求めることができます。

$$V_{1-}=\frac{R_1}{R_1+R_2}V_{out}$$

$$V_{2-}=\frac{R_2}{R_1+R_2}V_{in}$$
よって、$V_-$は以下のようになります。
$$V_{-}=V_{1-}+V_{2-}$$
$$V_-=\frac{R_1}{R_1+R_2}V_{out}+\frac{R_2}{R_1+R_2}V_{in}\cdots(2)$$
(1)式に(2)式を代入することで、$V_{out}$を求めることができます。
$$0=\frac{R_1}{R_1+R_2}V_{out}+\frac{R_2}{R_1+R_2}V_{in}$$
$$\frac{R_1}{R_1+R_2}V_{out}=-\frac{R_2}{R_1+R_2}V_{in}$$
$$V_{out}=-\frac{R_2}{R_1}V_{in}$$
ヌラーモデルを使った計算
反転増幅回路

これより、理想オペアンプをヌラーモデルに置き換えて、反転増幅回路を以下の通り計算してみます。
ヌラーモデルを用いることで、オペアンプの仮想短絡(イマジナリショート/バーチャルショート)の状態などを表すことができるので、計算を簡単にできるのです。
なお、ヌラーモデル自体の詳しい解説は以下の記事をご覧ください。
反転増幅回路(ヌラーモデル)
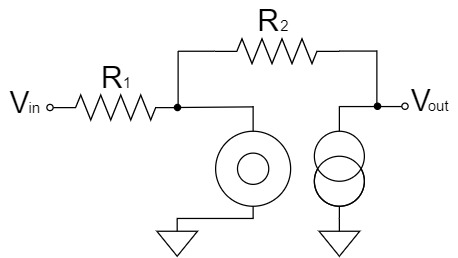
見やすくするために、回路図の形を変形させます。
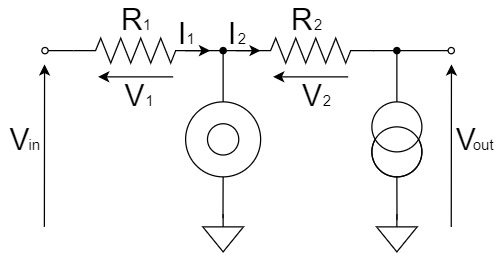
キルヒホッフの第1法則(電流則)より、$I_1$と$I_2$は以下の関係が成立します。
$$I_2=I_1$$
また、$I_1$と$I_2$をそれぞれ求めると以下のようになります。
$$I_1=\frac{V_1}{R_1}=\frac{V_{in}}{R_1}\cdots(1)$$
$$I_2=\frac{V_2}{R_2}=\frac{-V_{out}}{R_2}=-\frac{V_{out}}{R_2}\cdots(2)$$
(1)式と(2)式を$I_2=I_1$に代入すると、反転増幅回路の関係式を求めることができます。
$$-\frac{V_{out}}{R_2}=\frac{V_{in}}{R_1}$$
$$V_{out}=-\frac{R_2}{R_1}V_{in}$$
このように、ヌラーモデルを用いた反転増幅の等価回路から、関係式を算出することができました。
その他のオペアンプの回路例
当記事では、「オペアンプの反転増幅回路」について詳しく解説してきましたが、その他にもオペアンプには様々な回路が存在します。
以下の記事で、比較的よく使われるオペアンプの回路について紹介しているので、ぜひご覧ください。